The problems, concerning the provision of the quality of engineering education related to the insufficient level of the physical and mathematical preparation of the applicants, are considered. The imbalance between the number of applicants and the admission for the engineering majors at the national and regional levels is examined. On the basis of the content of the math tests of external independent evaluation of educational achievement and the procedures of forming the test results it is concluded that there is a discrepancy between the mathematical training of most applicants and the requirements necessary to provide the quality training of engineering personnel.
Monitoring and provision of the appropriate level of the prospective university students are fundamental to the quality assurance in education. The quality of training of the first year students of the university depends on several factors. The main points are the quality of secondary school education in the country and the region and the enrollment competition for a particular major in the university that makes it possible to choose the best applicants. Another factor is made up by several components which include the ratio of the number of the high school graduates in the country (region) and the size of the state order (volume license), the public image of the university, attractiveness training area (specialty) and its demand on the labor market (unfortunately the latter is not a prominent factor). In recent years, the total number of potential applicants has decreased by half - from 461 thousand people in 2008 to 293 thousand people in 2013 (Fig. 1). Although the proportion of students who choose the "exact sciences" has slightly increased (in 2008 49% of all the applicants took math exam and 7% took the physics test, in 2013 respectively 61% and 21% of students took those exams respectively), in absolute terms in 2013 only 61.4 thousand people had the external independent evaluation certificates in both mathematics and physics. Thus, the selection of the applicants for engineering specialties leaves a lot to be desired.
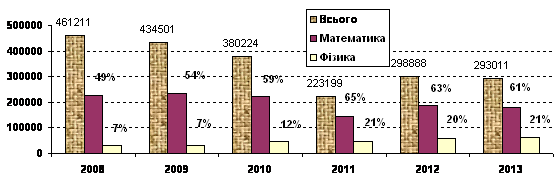
Figure 1. The number of potential applicants
Introduced in the 2008/09 academic year, the admission to universities on the results of an independent external evaluation of educational achievement, confirmed by the certificates of the Ukrainian Center for Educational Quality Assessment (UCEQA), radically changed the tried and tested approaches to the formation of the quality of the first-year students. For many years, ensuring of the proper physical and mathematical preparation of students NTUU "KPI" was the responsibility of the Faculty of Pre-University training. The classes on the faculty were conducted by the lecturers of the corresponding departments of the university. The participants of the course and high school students enriched their theoretical knowledge of physics and mathematics and acquired the skills to solve rather complicated problems. The faculty had a variety of tasks for the university entrance exams which had three levels according to the professional direction of the future specialties groups. It enabled the university to get their professionally oriented and well trained students.
Over the past 20 years, the university conducted a comprehensive analysis of the admission campaigns quality by comparing the results of entrance tests in mathematics and physics (since 2008 – the results of the EIT) and the first examination period (mathematics) and the second examination period (physics). In addition to general analysis, the influence of the type of pre-university training was investigated. Figure 2 shows the results of regression analysis of the interconnection of the higher mathematics test scores of the first examination period in the 1999/2000 academic year, the passing score of each student and the types of pre-university training.
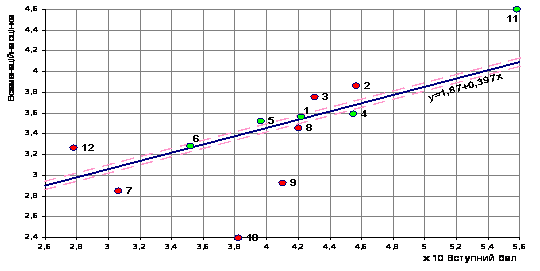
Figure 2. Statistical interconnection of the higher mathematics exam from the enrollment score and the type of pre-university training: 1 - the Faculty of Pre-University training ; 2 – lyceum form; 3 – external training on the Faculty of Pre-University training ; 4 - KPI Technical Lyceum; 5 - with a tutor; 6 - no additional training; 7 – on contract; 8 – medalists of secondary school; 9 – college honors degree; 10 – honors degree of technical school; 11 - the prize winners of the competitions; 12 - benefit recipients
This study shows that the Faculty of Pre-University training provided sufficiently high basic training, and the academic achievements of its graduates were not worse the results of those graduating with honors.
There were about 4000 graduates of the Faculty of Pre-University training who made up approximately 80% of the first year students. However, after the system of admission to universities on the basis of the results of external independent evaluation was implemented, the number of students of pre-university training decreased drastically (Fig. 3). In recent years, the number of students has begun to increase, due to the introduction of the accrual of additional points to the graduates of pre-university training system. It can be concluded that this decision MES was very reasonable.
This tendency reflected in the results of admission of students to the KPI (Fig. 4) can be traced in the first-year students. It can be concluded that the introduction of external independent evaluation has had some negative effects, namely a significant reduction in the number of students with high physical-mathematical training. Although in the past two years the situation with additional training students of the Faculty of Pre-University training has slightly improved, but the additional incentives and motivation of students will be necessary to restore the state that was before 2008.
It should be noted that the independent external evaluation provides the following advantages: sufficient opportunity to objectively evaluate the effectiveness of the pedagogical collectives of schools in general secondary education in Ukraine and assess the abilities of the graduates to mastering certain subjects, indirectly evaluate content, teaching methods and information and methodological support of these particular disciplines (unfortunately, these potential possibilities are not used by the authorities), and put an end to the discussions about corruption in universities.
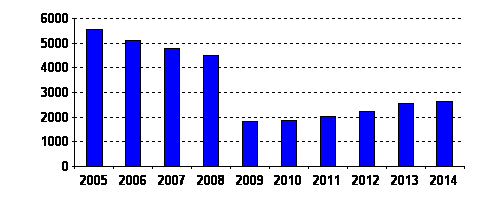
Figure 3. The number of the students of the Faculty of Pre-University
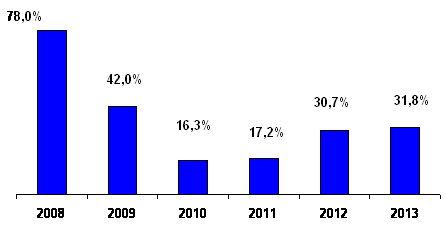
Figure 4. The number of the Faculty of Pre-University graduates among the first year students
Another benefit of the introduction of external independent evaluation is facilitating the access to training in the leading metropolitan for the high school graduates from the periphery, as evidenced by changes in the proportion of the first-year students of KPI from other cities over the past eight years (Fig. 5).
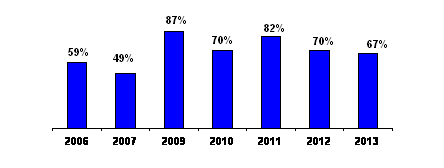
Figure 5. The share of first year students of KPI from other cities
The importance of this trend for KPI lies in the significant reduction of potential applicants in Kiev (Fig. 6). Only 3427 students Kyiv in 2013 took the mathematics and physics tests, and only 3,297 people received higher scores than the required minimum (124 points). The same year 4555 students were accepted in the university for the engineering majors, that is almost 40% higher than the number of potential applicants in the region.
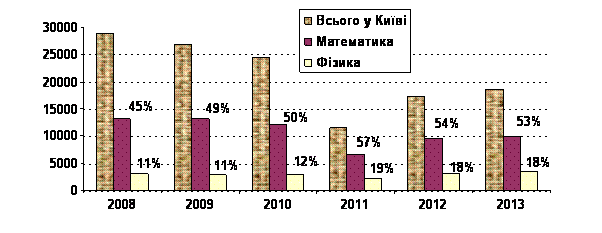
Figure 6. The number of prospective students in Kiev
The main criterion of the admission effectiveness must be ensuring the quality of preparation of students who were accepted in the university. To assess the quality of students who were enrolled in NTUU "KPI" as a result of the UCEQA certificates, for the third year we conducted the research to determine the academic progress of the first year students in higher mathematics and physics. The research was conducted by the approved methodology using probabilistic methods as well as the methods of correlation and regression analysis. You can see the results of studying the academic progress of 3928 first-year students in higher mathematics in the 2013/14 academic year.
The level of mathematical preparation of students of Ukraine was examined. The research was based on the report (the Report) Ukrainian Center for Educational Quality Assessment of the results of external independent evaluation in 2013.1
The background is the distribution of scores in mathematics tests of external independent evaluation for rating scale (Fig. 7).
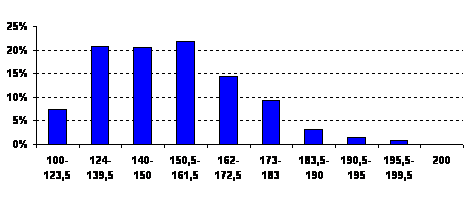
Figure 7. The distribution of rating scores in mathematics
At first glance, from this distribution it can be concluded that the level of mathematical preparation of the students of Ukraine is sufficient. However, a more thorough examining of the Report raises doubts about this conclusion. The reason for this is the primary information, regarding the results of external independent evaluation - distribution test scores (Fig. 8). The discrepancy between two distributions (Fig. 7 and Fig. 8) is associated with nonlinear transformation of the test scores in rating.
div align="center">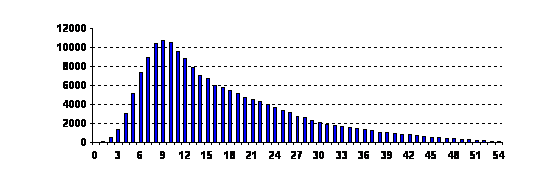
Figure 8. The distribution of test scores in mathematics
In the report it was noted that " The formation of the rating scale was carried out on the basis of understanding that it is:
• close to the reference scale with the average results of each item;
• standardized. The distribution of high school graduates at this scale is about the same regardless of the subject tests;
• rating. The applicant, who got more test scores at a certain subject, will not have a lower assessment than the applicant, who got lower scores at the same subject.
• fair. The applicants, who received an equal number of test points at a particular subject, have the same scale for this rating.
Using the rating scale provided an opportunity to identify and rank the high school graduates based on how well they performed the test. "
However, the actual implementation of these provisions is questionable. It should be noted that the mathematics test was conducted in two sessions and the schedules of point changes were different (Fig. 9). It creates the unequal conditions of external independent evaluation for the students that were tested in different sessions. For example, the student, who scored 16 points in the first test session, receives 150.5 rating points, for the same 16 test points in the second session the student gets 158 ranking points. The difference is 7.5 points, which can be crucial when applying to the universities. Thus, the mentioned characteristics of "rating" and "fair" are not always typical of the formation of rating scale.
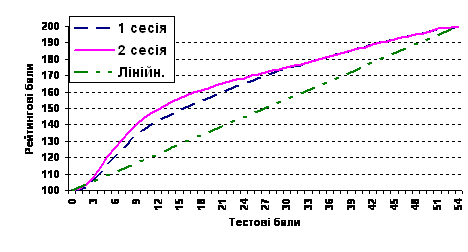
Figure 9. The conversion of test scores into rating ones
It should also be noted that the nonlinear transformation of the points distorts the real picture of the level of Ukrainian high school graduates of a particular subject. To illustrate this we give the distribution of rating points for the math using nonlinear as well as linear laws (Figure 10).
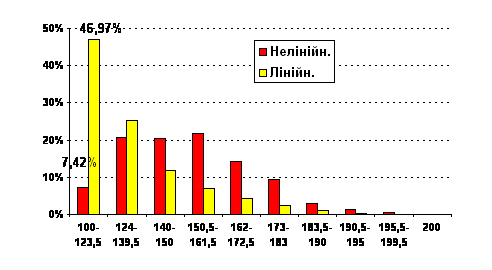
Figure 10. The comparison of the distributions of the rating scores based on linear and nonlinear laws
Fig. 10 implies that the "unsatisfactory" or less than 124 rating points, were not 7,42% but almost (if linear transformation is concerned) 47% of applicants!
The use of a rating scale of 100-200 points is surprising. A rating scale of 0-100 points seems to be more logical. However, the current situation enables the high school graduate who failed his mathematics test to answer the question about his academic success in this subject that his results are average that is 100 of 200.
There is a question about the choice of the allowable minimum score as 124 which enables the students to participate in the competition of the certificates. What influenced this choice? Is that - 62% of the 200 points, or 24% of 100, or 13% (7 points) on the scale of test scores? In pedagogy it is usually considered that the student can receive a positive assessment having mastered at least 60% of the planned training results of the certain subject. By using the closed test one should take into account the probability of guessing answers. The structure of the mathematics test consists of 36 simple tasks with a choice of one correct answer (1 of 5) which gives 1 point to a high school graduate (closed tests) and 9 tasks of open form with a short answer ( the right one will give a high school graduate 2 points). Figure 11 illustrates the graph of interconnection of the share of knowledge and the number of rating scores for the mentioned structure of the mathematics test on the condition of confidence probability of 0.8 (confidence interval is shown by dotted line).
div align="center">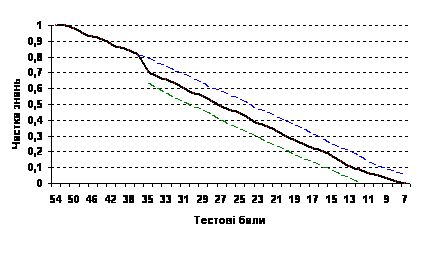
Figure 11. The interconnection of knowledge share and test scores
This graph shows that the assessment of "satisfactory" corresponds to 31 test score (175.5 rating points in nonlinear transformation), assessment of "good" (knowledge share - 75%) - 36-41 test points (181,5-187,5 rating points) and assessment "excellent" (knowledge share - 90%) – at least 42 test points (189-200 rating points).
Taking these boundary values of figures on the distribution of test scores of all high school graduates of Ukraine (Figure 8), we have the following meanings: absolute indicator of success AS = 11.9%, and the quality of success QS = 7.1%. Consequently, actual results of external independent evaluation in mathematics are extremely low.
Let us analyze the hypothesis of possibility of the tasks of high complexity at external independent evaluation. Here are some examples of tasks with a choice of one correct answer:

By the way, doing the last task right you can get 4 points!
From these examples it can be concluded that the first 36 tasks with a choice of one correct answer iare quite simple. Unfortunately, the report for 2013, in contrast to reports from previous years does not provide the percentage of students who completed each task, but the average data are: average difficulty of the test tasks (average percentage of) - 31.76%; the average number of test points - 17.07. We can therefore agree with the findings outlined in the report: "... the third of the participants who took the mathematics test do not possess the formed basis ability of transforming the simplest rational expressions. The applicants do not have the skills of simplifying logarithmic expressions and don not know the relevant formulas,… most part of external independent evaluation participants did not have the necessary knowledge on the basics of trigonometry and did not know axioms, basic theorems and formulas of geometry.
Thus, the lack of basic knowledge and skills the students should acquire while studying mathematics (before the 7th grade), algebra and geometry in school leads to losing the ability to master the course material with high school mathematics even at the secondary level educational achievements. "
The conclusions about the mass mathematical preparation of students of Ukraine are quite sad but fair.
Taking the above information into account, there is a question about the quality of studying of the first-year students of the university. The primary information is the distribution points of external independent evaluation in mathematics by the rating scale of the pupils and the students of NTUU "KPI" (Fig. 12).
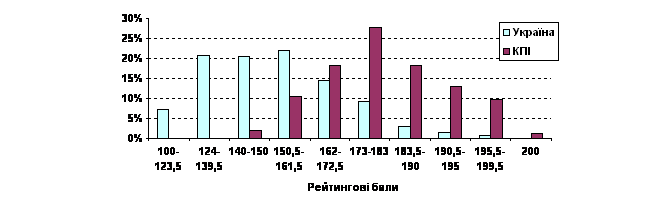
Figure 12. The distribution of the rating scores of the KPI students and high school graduates in Ukraine
From Figure 12 it can be concluded (base of analysis is the results of 4259 students of external independent evaluation), that the students who were accepted to KPI are the best. This conclusion is confirmed by the fact that among first-year students 57 people have 200 points of external independent evaluation in mathematics, making up 42.9% of students in Ukraine.
In NTUU "KPI" a system of the management of training quality was created, the part of which includes an input control for each discipline, the rating system evaluating the success of student learning, calendar intermediate (8th and 14th weeks of the semester) certification of the students and appropriate organizational and didactic measures. Input controls of the level of training of the students are conducted during the first practical lessons of higher mathematics based on high school mathematics program, and aim at obtaining the information on the initial level of mathematical training of the first year students and development of measures to ensure their successful training.
The department of Mathematics NTUU "KPI" has an extensive experience in teaching high school graduates in the Faculty of Pre-University training and accordingly a large base of control tasks for the diagnosis of preparation. Figure 13 shows the distribution of input control ratings of the students who were accepted to the university on the first course in 2013. Evaluation was conducted at the six-point scale, score "2" corresponds to the implementation of less than 50% of the problem, "0" - less than 10%.
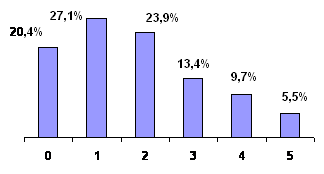
Figure 13. The results of input control
In view of the information shown above the results of input control are not unexpected: absolute performance is AS = 28.7%, quality success QS = 15.2%.
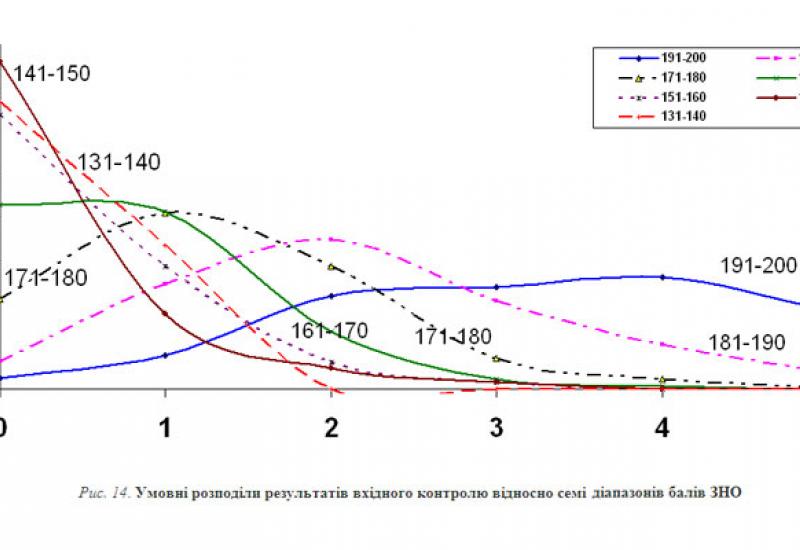
More detailed information is of greater interest, to be more exact the connection of these results with external independent evaluation scores is interesting to examine. Figure 14 grants conditional (acquired by students on the basis of external independent evaluation points) distribution of the input control. The correlation of the results with input control with external independent evaluation scores is quite high (R = 0,66).
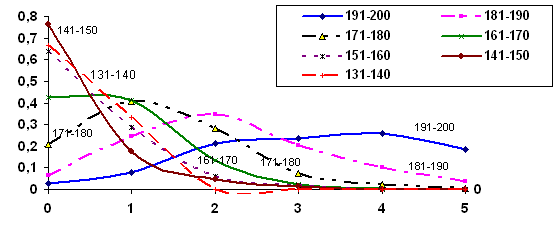
Figure 14. The conditional distributions of the input control results in relation to 7 ranges of external independent evaluation scores
The shown graphs show that 131-170 points correspond to the assessment "0" of input control (carrying no more than 10% of the task). Most students who had received 171-180 points during external independent evaluation received "1" (up to 20% of the tasks) on the input control, and those who had 181-190 points – got "2" (30% of the job). Unfortunately, even the student with excellent results (191-200 points at external independent evaluation) showed quite low results - AS = 68%, QS = 44.3%. All this confirms the findings mentioned above that a positive assessment must begin with 175-180 points. It is the trigger of a recommendation from the leading universities of Ukraine, who have to prepare elite professionals – it is necessary to establish the minimum rating score in mathematics of at least 170. The question naturally arises: where to get the required number of students?
Similar problems were pointed out by the rector of Moscow State University V.A. Sadovnichy in the newspaper "Search": "With the tests our university arranges annually during the first year only less than half the students manage to cope. The level of school training has become lower, particularly in physics, mathematics and chemistry. This is a big problem, and it should be immediately addressed. "
The main purpose of the performance criterion of the university admissions campaign is to ensure the enrollment of students that can cope with higher education programs. Therefore, the analysis of results of examinations is an important part of quality provision in the university. In Figure 15 there are results of the exam in higher mathematics (the first attempt) at the first session of 2013 students receive.
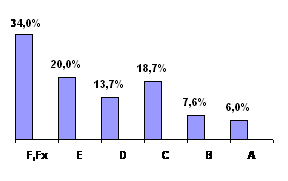
Figure 15. The results of high mathematics exam
This level of mastering of higher mathematics cannot be considered satisfactory - absolute success is 66%, and the quality of success only 32.3%. These results are predictable, if we take into account the distribution of test scores of students and the results of input control. Naturally, after passing the exam for the second time most unsatisfactory evaluations are replaced with an "E" enabling an absolute success the approach 90-95%, but the figure does not change the quality and academic success does not meet accreditation requirements.This indicates that the results of external independent evaluation in mathematics cannot ensure that the students will be able to grasp higher mathematics in the university.
The correlation coefficient of the examination scores assessments of external independent evaluation is only 0.45. Intuitively the origins of pre-correlation can be seen according to conditional distributions matrix ratings(Fig. 16).
Test scores
|
External independent evaluation results |
|
A |
B |
C |
D |
E |
Fx, F |
|
200-191 |
0,159 |
0,153 |
0,273 |
0,157 |
0,116 |
0,143 |
|
|
190-181 |
0,055 |
0,098 |
0,239 |
0,147 |
0,184 |
0,277 |
|
|
180-171 |
0,024 |
0,038 |
0,158 |
0,167 |
0,231 |
0,381 |
|
|
170-161 |
0,007 |
0,01 |
0,086 |
0,21 |
0,276 |
0,511 |
|
|
160-151 |
0 |
0,003 |
0,067 |
0,082 |
0,247 |
0,602 |
|
|
150-141 |
0 |
0 |
0,032 |
0,048 |
0,27 |
0,651 |
|
|
140-131 |
0 |
0 |
0 |
0,333 |
0,667 |
0 |
|
|
|
|||||||
Figure 16. The matrix of conditional distributions of the scores
Among students who had more than 190 points according to their certificates, only 31.2% confirmed the high level of training (grades A, B), and 41.6% received low results (D, E, FX), including an assessment FX which was obtained by 14.3% of students. Almost every third student with a maximum score of 200 (!) was rated with a D and below, and the students with scores 190-181 and 180-171 received E or FX, respectively 46.1% and 61.2%. More than half of the students who received the score of at least 170 were assessed with "unsatisfactory" during the exam in the university. And it is natural, because according to the testing scale 170 points are given to the students who solved only half the tests.
The prospect of turning such students into the elite engineers, who will be able to design a modern competitive technology, is highly questionable. Another educational problem - when the study group is reaches "critical share" (about 50%) of weak students – it negatively influences the overall level of teaching of the material, the level of requirements and demands. This affects all the students.
Conclusions:
- The level of mathematical preparation of students of Ukraine is alarming. The measures aimed at improving of knowledge of the students in natural studies should be implemented in the nearest time to improve the natural training students.
- It is desirable to revive the activities of the Faculty of Pre-University training and enable the variety of training forms: full-time, part-time and distance. It is necessary to stimulate their activities. This will allow at the first phase significant improvement of the training of the high school graduates in mathematics, physics, chemistry and other subjects.
- The results of studies of students with higher math scores are barely related to relevant external independent evaluation certificates, because the content of the relevant tests need to be refined and to it a predictive component must be added.
- The system of the scaling results of external independent evaluation is not clear, it masks the true level of knowledge of the high school graduates and needs improvement, namely the use of a linear transformation of the test points within a certain discipline in a standard scale of the size of 100 points.
- In order to ensure the effective preparation of elite engineering staff in the leading universities it will be appropriate to establish the minimum score of certificates of high school graduates in mathematics and physics at least 170 (in the current system of rating points) and additional creative tests should be an option.
- The leading universities aimed at the formation of the intellectual elite of the state, should have the right to arrange additional creative tests that will allow them to select their high school graduates really willing and able to master the deep fundamental knowledge.
- In higher education establishments there should be an effective system of individual training activities of the students which should realize calendar prognostic abilities of the certifications of the students and the rating systems of assessment of the knowledge of the students.
References:
- Ukrainian Center of Educational Quality Assessment. The official report on external independent evaluation of educational achievements of the high school graduates of the educational establishments of Ukraine in 2013. - Access: http://www.testportal.gov.ua/reports/