Розглядаються проблеми забезпечення якості інженерної освіти, пов’язані з недостатнім рівнем фізикоматематичної підготовки абітурієнтів. Обговорюється ситуація дисбалансу кількості абітурієнтів і обсягів прийому на інженерні напрями підготовки на всеукраїнському й регіональному рівнях. На підставі аналізу змісту тестових завдань з математики зовнішнього незалежного оцінювання навчальних досягнень та процедур формування результатів тестування робиться висновок про невідповідність математичної підготовки більшості абітурієнтів вимогам забезпечення підготовки якісних інженерних кадрів.
Однією з важливих складових системи забезпечення якості освіти є моніторинг та забезпечення належного рівня підготовки абітурієнтів. Якість підготовки студентів першого курсу університету залежить від декількох факторів. Це, перш за все, якість загальної середньої освіти у державі та регіоні, а також конкурс на конкретний напрям підготовки в університеті, який дозволяє відібрати кращих абітурієнтів. Останній фактор залежить від багатьох чинників: співвідношення кількості випускників шкіл у державі (регіоні) та розміру держзамовлення (ліцензійного обсягу), іміджу університету, привабливості напряму підготовки (спеціальності) та його затребуваності на ринку праці (на жаль останнє не є визначним чинником). За останні роки загальна кількість потенційних абітурієнтів зменшилася у півтори рази, з 461 тис. у 2008 р. до 293 тис. у 2013 р. (рис. 1). Хоча частка школярів, які вибирають «точні науки» трохи збільшується (у 2008 р. математику складали 49 % від загальної кількості абітурієнтів, а фізику – 7 %; у 2013 році відповідно 61 % та 21 %) , в абсолютному вимірі в 2013 році мають сертифікати ЗНО з фізики і математики всього лише 61,4 тис. осіб. Таким чином, база вибору підготовлених абітурієнтів для навчання з інженерних спеціальностей є вкрай малою.
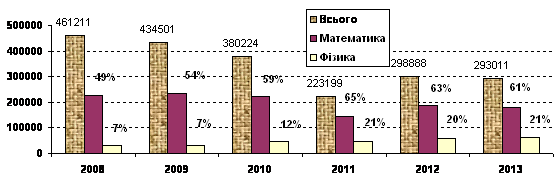
Рис. 1. Кількість потенційних абітурієнтів
Запроваджений з 2008/09 навчального року прийом до ВНЗ за результатами зовнішнього незалежного оцінювання навчальних досягнень, що підтверджені сертифікатами Українського центру оцінювання якості освіти (УЦОЯО) докорінно змінив напрацьовані підходи щодо формування якісного складу студентів першого курсу. Багато років завдання забезпечення належної фізикоматематичної підготовки абітурієнтів НТУУ «КПІ» вирішував факультет доуніверситетської підготовки (ФДП). На факультеті заняття проводили викладачі відповідних кафедр університету. Слухачі, школярі випускного класу, поглиблювали теоретичні знання з фізики і математики, набували вмінь розв’язувати достатньо складні задачі. Факультет мав значну базу варіантів завдань для вступних випробувань до університету, диференційовану за трьома рівнями відповідно до фахової спрямованості груп майбутніх спеціальностей. Все це забезпечувало університету можливість отримувати «своїх», професійно орієнтованих й достатньо підготовлених абітурієнтів.
Протягом останніх 20 років в університеті проводиться комплексний аналіз якості вступних кампаній шляхом порівняння результатів вхідних випробувань з математики і фізики (з 2008 року – результатів зовнішнього незалежного оцінювання) та підсумків першої сесії (з математики) і другої сесії (з фізики). Окрім загального аналізу досліджувався вплив виду доуніверситетської підготовки. На рис.2 наведено результати регресійного аналізу залежності екзаменаційних оцінок з вищої математики у першій сесії у 1999/2000 навчальному році від вступного балу та за видами доуніверситетської підготовки.
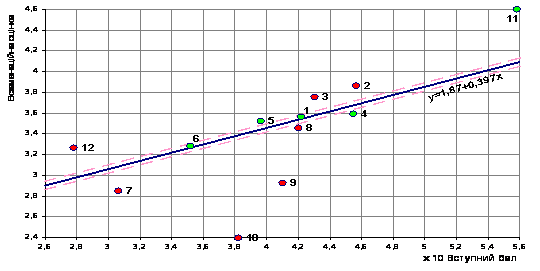
Рис. 2. Статистична залежність результатів екзамену з вищої математики від вступного балу та виду доуніверситетської підготовки:
1 – ФДП; 2 – ліцейні класи; 3 – екстерн ФДП; 4 – технічний ліцей КПІ; 5 – з репетитором; 6 – без додаткової підготовки; 7 – контрактники; 8 – медалісти середньої школи; 9 – диплом з відзнакою технікуму; 10 – диплом з відзнакою ПТУ; 11 – призери олімпіад; 12 – пільговики
З цього дослідження випливає, що ФДП забезпечував досить високу базову підготовку, його випускники не поступалися за якістю навчання навіть медалістам середньої школи.
Кількість слухачів ФДП була приблизно 4 тисячі, ними комплектувалося до 80 % студентів першого курсу. Але, після запровадження системи прийому до ВНЗ за результатами ЗНО, кількість слухачів системи доуніверситетської підготовки різко зменшилася (рис. 3). Тільки за останні роки почалося збільшення чисельності слухачів, що пов’язано із запровадженням нарахування додаткових балів випускникам системи доуніверситетської підготовки. Можна зробити висновок про доцільність цього рішення МОН.
За результатами прийому студентів до КПІ (рис.4) видно, що ця тенденція віддзеркалюється також у складі студентів першого курсу. З цього можна зробити висновок, що запровадження ЗНО мало певні негативні наслідки, а саме, значне зменшення чисельності студентів із вихідною підвищеною фізикоматематичною підготовкою. Хоча в останні два роки ситуація з додатковою підготовкою абітурієнтів на ФДП трохи покращилася, для відновлення стану, який був до 2008 року, потрібні додаткові стимули та мотивація абітурієнтів.
Треба зазначити, що зовнішнє незалежне оцінювання надає: можливість достатньо об’єктивно оцінювати ефективність роботи педагогічних колективів шкіл, в цілому рівень середньої освіти в Україні та якість засвоєння випускниками окремих навчальних дисциплін, опосередковано оцінити зміст, методику викладання та інформаційнометодичне забезпечення цих дисциплін (на жаль ці потенційні можливості органами управління освітою не використовуються) і, нарешті, припинити розмови про корупцію у ВНЗ.
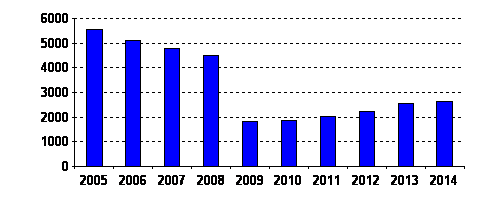
Рис. 3. Кількість слухачів ФДП КПІ
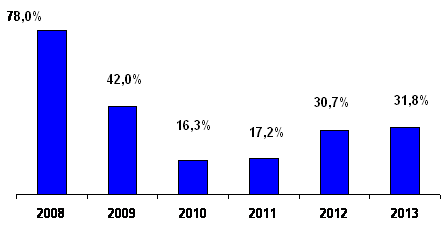
Рис. 4. Частка випускників ФДП у складі студентів першого курсу КПІ
Ще одним позитивом впровадження ЗНО є полегшення доступу до навчання у провідних столичних ВНЗ абітурієнтів з периферії, що підтверджується змінами частки студентів першокурсників КПІ з інших міст за останні вісім років (рис. 5).
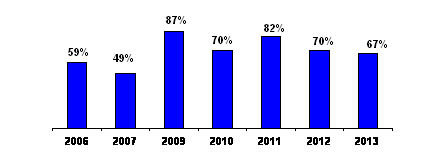
Рис. 5. Частка студентів з інших міст на першому курсі КПІ
Важливість цього для КПІ обумовлена тенденцією значного зменшення потенційних абітурієнтів у Києві (рис. 6). Тільки 3427 школярів Києва складали у 2013 році ЗНО з математики й фізики і лише 3297 осіб отримали вище балів ніж необхідний мінімум (124 бали). У цьому ж році на напрями інженерної підготовки в КПІ було прийнято 4555 студентів, що майже на 40 % перевершує регіональну кількість потенційних абітурієнтів..
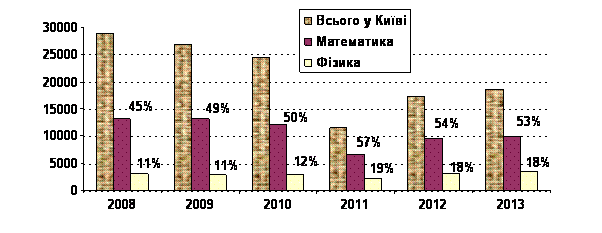
Рис.6. Кількість потенційних абітурієнтів у Києві
Основним критерієм щодо ефективності системи прийому має бути забезпечення належної якості підготовки абітурієнтів, які прийняті до навчання у ВНЗ. З метою оцінювання якості абітурієнтів, які були зараховані до НТУУ «КПІ» за конкурсом балів сертифікатів УЦОЯО, нами вже третій рік проводиться дослідження щодо успішності навчання студентів першого курсу з вищої математики і фізики. Дослідження проводяться за апробованою методикою з використанням методів імовірнісного, кореляційного та регресійного аналізу. До Вашої уваги пропонуємо результати дослідження успішності навчання з вищої математики 3928 студентів першого курсу 2013/14 навчального року.
Поперше, проаналізуємо рівень математичної підготовки школярів України, узявши за основу звіт (далі Звіт) Українського центра оцінювання якості освіти про результати зовнішнього незалежного оцінювання у 2013 році.
Вихідною інформацією є розподіл балів ЗНО з математики за рейтинговою шкалою (рис. 7).
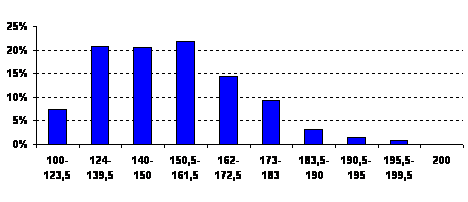
Рис. 7. Розподіл рейтингових балів з математики
На перший погляд, з цього розподілу можна зробити висновок про достатній рівень математичної підготовки школярів України. Але більш поглиблене ознайомлення зі Звітом дає основу для сумніву щодо такого висновку. Приводом до цього є первинна інформація щодо результатів оцінювання ЗНО – розподіл тестових балів (рис. 8). Невідповідність двох розподілів (рис.7 та рис.8) пов’язана з нелінійною трансформацією тестових балів у рейтингові.
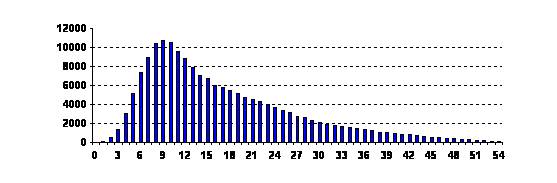
Рис. 8. Розподіл тестових балів з математики
У Звіті зазначено, що «Формування рейтингової шкали здійснювалося на основі розуміння того, що вона є:
- наближеною до еталонної шкали з середнім значенням результатів із кожного предмета;
- стандартизованою. Розподіл абітурієнтів за цією шкалою є приблизно однаковим незалежно від предмета тестування;
- рейтинговою. Абітурієнт, який набрав з певного предмета більше тестових балів, матиме за цією шкалою оцінку не нижчу ніж той, хто набрав з цього предмета меншу кількість балів;
- справедливою. Абітурієнти, які набрали однакову кількість тестових балів із певного предмета, мали за цією шкалою однакову оцінку.
Використання рейтингової шкали дало можливість визначити та ранжувати абітурієнтів залежно від того, наскільки успішно вони виконали тест».
Щодо реального виконання цих положень виникає сумнів. Необхідно зазначити, що тестування з математики проводилося двома сесіями і графіки перетворень балів були різними (рис. 9). Це робить нерівними умови ЗНО для школярів, що проходили тестування у різних сесіях. Наприклад, школяр, який набрав 16 тестових балів у першій сесії отримує 150,5 рейтингових балів, за ті ж 16 тестових балів у другій сесії школяр отримує вже 158 рейтингових балів. Різниця складає 7,5 балів, що може бути вирішальним при прийомі до ВНЗ. Таким чином, задекларовані «рейтинговість» і «справедливість» не виконуються.
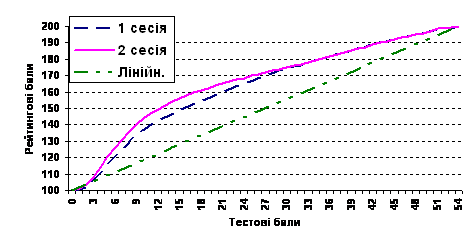
Рис. 9. Графіки перетворення тестових балів у рейтингові
Необхідно також зазначити, що нелінійне перетворення балів викривляє уявлення про реальний рівень підготовки школярів України з певного предмета. Для ілюстрації цього наведемо розподіл рейтингових балів з математики за використаним нелінійним, а також лінійним законами (рис.10).
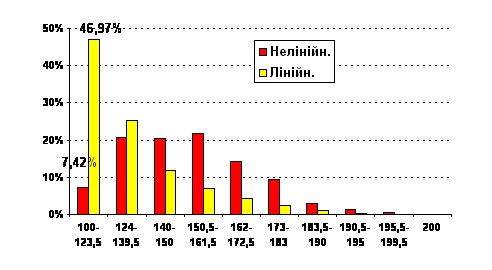
Рис. 10. Порівняння розподілів рейтингових балів, розрахованих за нелінійним і лінійним законами
З рис. 10 випливає, що «незадовільно», або менш ніж 124 рейтингових балів, отримали не 7,42 %, а майже (при лінійному перетворенні) 47 % абітурієнтів!
Подив викликає також використання рейтингової шкали 100200 балів. Чому не 0100? Пропоную варіант – надати можливість абітурієнтуневдасі на запитання – «Як твої успіхи з математики?», відповісти – «Середні, отримав 100 балів із 200».
Інше питання виникає відносно вибору 124 балів як межі допуску абітурієнта до конкурсу у ВНЗ. Які міркування вплинули на цей вибір? Це що – 62 % від 200 балів, або 24 % від 100, або 13 % (7 балів) від шкали тестових балів? Звичайно у педагогіці вважається, що позитивну оцінку учень може отримати за умови володіння не менш ніж 60 % запланованих результатів навчання з певного предмета. При використанні закритих тестів потрібно врахувати ймовірність вгадування відповідей. Структура тесту з математики містить 36 простих завдань з вибором однієї правильної відповіді (1 з 5х) з оцінкою 1 бал (закриті тести) та 9 завдань відкритої форми з короткою відповіддю з оцінкою 2 бали. На рис. 11 надано графік залежності частки знань від кількості рейтингових балів для вищезазначеної структури тесту з математики за умови довірчої вірогідності 0,8 (довірчій інтервал надано пунктиром).
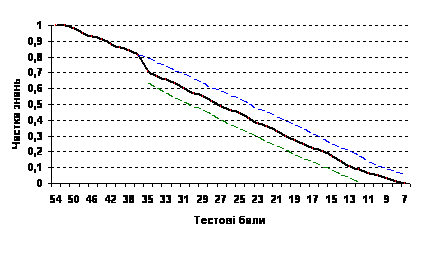
Рис. 11. Залежність частки знань від кількості рейтингових балів
З цього графіку випливає, що оцінці «задовільно» відповідає 31 тестовий бал (175,5 рейтингових балів при нелінійній трансформації), оцінці «добре» (частка знань – 75 %) – 3641 тестових балів (181,5187,5 рейтингових балів), а оцінці «відмінно» (частка знань – 90 %) – не менш ніж 42 тестових балів (189200 рейтингових балів).
Узявши з основу ці межові показники з розподілу тестових балів всіх абітурієнтів України (рис.8), маємо такі значення: показник абсолютної успішності АУ=11,9%, а якість успішності ЯУ=7,1 %. Отже, реальні результати ЗНО з математики вкрай низькі.
Проаналізуємо гіпотезу можливої високої складності завдань ЗНО. Наведемо декілька прикладів завдань з вибором однієї правильної відповіді:

До речі, за останнє завдання можна отримати 4 бали!
З цих прикладів випливає, що перші 36 завдань з вибором однієї правильної відповіді досить прості. На жаль, у Звіті за 2013 рік, на відміну від звітів за попередні роки, не надано відсоток абітурієнтів, які виконали кожне завдання, але середні дані такі: середня складність завдань тесту (середній відсоток виконання) – 31,76 %; середня кількість тестових балів – 17,07. Тому можна погодитися з висновками, наведеними у Звіті: «… в третини учасників ЗНО з математики не сформовані базові уміння з перетворення найпростіших раціональних виразів. … абітурієнти не володіють уміннями спрощення логарифмічних виразів і не знають відповідних формул, …значна частина учасників тестування не має необхідних знань з основ тригонометрії, не знають аксіом, основних теорем і формул стереометрії.
Отже, відсутність базових знань та умінь, які учні повинні набути під час навчання математиці (до 7 класу), алгебрі та геометрії в основній школі, призводить до втрати можливості опанувати навчальний матеріал з математики старшої школи навіть на середньому рівні навчальних досягнень».
Досить сумні і справедливі висновки щодо масової математичної підготовки школярів України.
З урахуванням вищезазначеного виникає питання щодо якості навчання студентів перших курсів. Первинною інформацією є розподіл балів ЗНО з математики за рейтинговою шкалою школярів України та студентів НТУУ «КПІ» (рис.12).
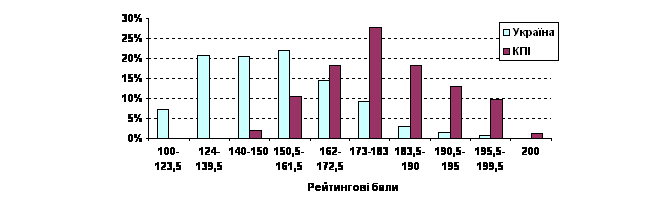
Рис. 12. Розподіл рейтингових балів ЗНО з математики школярів України та студентів КПІ
З рис. 12 можна зробити висновок (базою аналізу є результати ЗНО 4259 студентів), що до КПІ вступили кращі школярі. Цей висновок підтверджує й те, що серед студентів першого курсу 57 осіб мають 200 балів ЗНО з математики, що складає 42,9 % таких школярів України.
У НТУУ «КПІ» створено систему управління якістю навчання, частина якої містить вхідний контроль з кожної навчальної дисципліни, рейтингову систему оцінювання успішності навчання студентів, календарну проміжну (на 8му та 14му тижнях семестру) атестацію студентів та відповідні організаційні та дидактичні заходи. Вхідний контроль рівня підготовки студентів проводиться на перших практичних заняттях з вищої математики за програмою математики середньої школи, та має на меті отримання інформації щодо вихідного рівня математичної підготовки першокурсників і розроблення системи заходів для забезпечення їхнього успішного навчання.
Кафедри вищої математики НТУУ “КПІ” мають багатий досвід навчання абітурієнтів у ФДП та відповідно велику базу контрольних завдань для діагностики рівня підготовки. На рис. 13 наведено розподіл оцінок вхідного контролю студентів, які були прийняти на перший курс у 2013 році. Оцінювання проводилося за шестибальною шкалою, оцінка «2» відповідає виконанню менш ніж 50 % завдання, «0» – менш ніж 10 %.
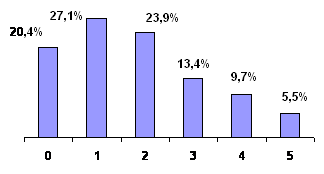
Рис. 13. Результати вхідного контролю
З урахуванням вищезазначеного – результати вхідного контролю очікувані, абсолютна успішність складає АУ=28,7 %, якість успішності ЯУ=15,2 %.
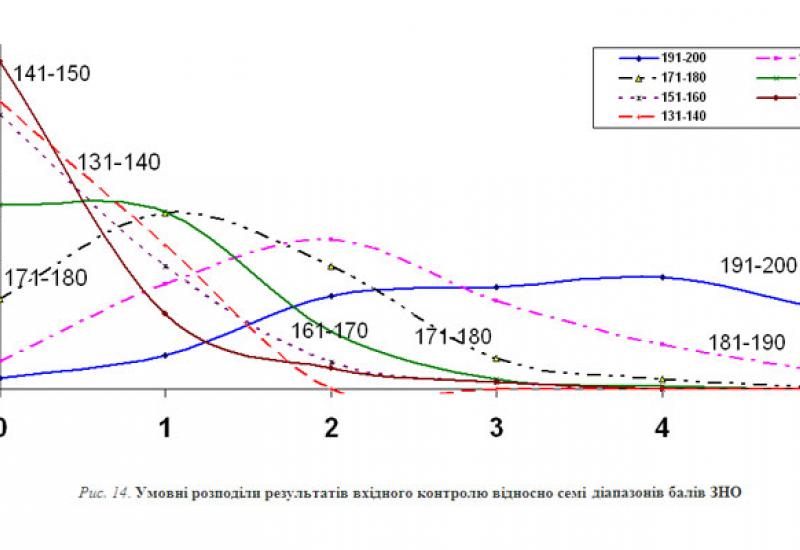
Цікава більш детальна інформація, а саме зв'язок цих результатів із балами ЗНО. На рис. 14 надані умовні (за умовою отриманих студентами певних балів ЗНО) розподіли результатів вхідного контролю. Кореляція результатів вхідного контролю із балами ЗНО достатньо висока (R=0,66).
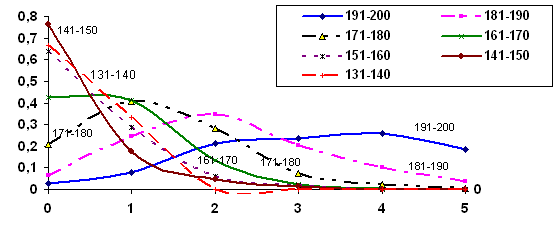
Рис. 14. Умовні розподіли результатів вхідного контролю відносно семі діапазонів балів ЗНО
З наданих графіків випливає, що у межах 131170 балів медіана розподілів належить оцінці «0» вхідного контролю (виконання не більш ніж 10 % завдання). Більшість студентів, які мали 171180 балів ЗНО отримали на вхідному контролі оцінку «1» (до 20 % виконання завдання), а ті, що мали 181190 балів – оцінку «2» (до 30% виконання завдання). На жаль, навіть відмінники (191200 балів ЗНО) показали достатньо низький результат – АУ=68 %, ЯУ=44,3 %. Все це підтверджує вищезазначені висновки, що позитивне оцінювання має починатися з 175180 балів. З цього випливає рекомендація для провідних університетів України, які мають готувати елітних фахівців, – встановити у правилах прийому мінімальний рейтинговий бал з математики на рівні не менш ніж 170. Природно виникає питання: де взяти необхідну кількість таких школярів?
Аналогічні проблеми зазначив ректор МДУ В.А. Садовничий у газеті «Поиск»: «З контрольними роботами, які університет щорічно проводить на першому курсі, впоралися менше половини студентів. Рівень шкільної підготовки став нижче, особливо з фізики, математики, хімії. Це велика проблема, і необхідно негайно вживати заходів щодо її вирішення».
Основною метою й критерієм ефективності приймальної кампанії до університетів є забезпечення прийому студентів, здатних засвоювати програми вищої освіти. Тому аналіз результатів екзаменів є важливою складовою університетської системи забезпечення якості. На рис.15 надані результати екзамену з вищої математики (за першою спробою) на першій сесії студентів 2013 року прийому.
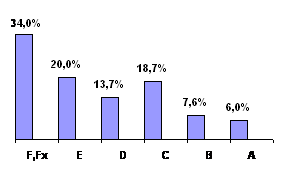
Рис. 15. Результати екзамену з вищої математики
Такий рівень засвоєння вищої математики не можна вважати задовільним – абсолютна успішність дорівнює 66 %, а якість успішності лише 32,3 %. Ці результати є передбачуваними, якщо брати до уваги розподіл тестових балів школярів та результати вхідного контролю. Звичайно за рахунок двох перескладань екзамену більшість незадовільних оцінок заміняються, як правило, на «Е», тому абсолютна успішність наближається до 9095 %, але показник якості успішності не змінюється і не відповідає акредитаційним вимогам. Це свідчить про те, що результати ЗНО з математики практично не гарантують спроможність студентів засвоювати вищу математику у ВНЗ.
Коефіцієнт кореляції екзаменаційних оцінок з балами ЗНО складає тільки 0,45. Наочно витоки декореляції виявляються з відповідної матриці умовних розподілів оцінок (рис. 16).
| Екзаменаційні оцінки | |||||||
| Бали сертифікатів | A | B | C | D | E | Fx, F | |
| 200191 | 0,159 | 0,153 | 0,273 | 0,157 | 0,116 | 0,143 | |
| 190181 | 0,055 | 0,098 | 0,239 | 0,147 | 0,184 | 0,277 | |
| 180171 | 0,024 | 0,038 | 0,158 | 0,167 | 0,231 | 0,381 | |
| 170161 | 0,007 | 0,01 | 0,086 | 0,21 | 0,276 | 0,511 | |
| 160151 | 0 | 0,003 | 0,067 | 0,082 | 0,247 | 0,602 | |
| 150141 | 0 | 0 | 0,032 | 0,048 | 0,27 | 0,651 | |
| 140131 | 0 | 0 | 0 | 0,333 | 0,667 | 0 | |
| Рис.16. Матриця умовних розподілів оцінок | |||||||
Серед студентів, які мали у сертифікаті більше 190 балів, тільки 31,2 % підтвердили високий рівень підготовки (оцінки А, В), а 41,6 % отримали низькі результати (D, E, FХ), у тому числі оцінку FХ мали 14,3 % студентів. Майже кожен третій студент з максимальним балом 200 (!) отримав оцінку D й нижче, а серед студентів з балами 190181 та 180171 оцінки Е або FХ отримали відповідно 46,1 % та 61,2 %. Більше половини студентів з балом сертифіката менше 170 на екзамені отримали «незадовільно». І це закономірно, тому що шкала ЗНО передбачає надання 170 балів у разі розв’язування тільки половини тестових завдань.
Можливість підготувати з таких студентів елітних інженерів, спроможних спроектувати сучасну конкурентоспроможну техніку, викликає великий сумнів. Ще одна педагогічна проблема – коли в навчальній групі збирається «критична частка» (біля 50 %) слабких студентів – знижуються загальний рівень викладання навчального матеріалу, рівні вимог і вимогливості. Від цього страждають всі студенти.
Висновки:
- Рівень математичної підготовки школярів України викликає тривогу. Необхідно найскоріше вживати систему заходів щодо покращення природничої підготовки школярів.
- Бажано відродити діяльність підрозділів довузівської підготовки з різними формами навчання: денною, заочною та дистанційною. Стимулювати їхню діяльність. Це дозволить на першому етапі значно покращити підготовку абітурієнтів з математики, фізики, хімії тощо.
- Результати навчання студентів з вищої математики слабко пов’язані з балами відповідних сертифікатів ЗНО, тому зміст відповідних тестових завдань потрібно доопрацювати та додати певну прогностичну складову.
- Система шкалювання результатів ЗНО не є прозорою, маскує справжній рівень підготовки абітурієнтів й потребує удосконалення, а саме використання лінійної трансформації тестових балів з певної навчальної дисципліни у стандартну шкалу розміром 100 балів.
- З метою забезпечення підготовки елітних інженерних кадрів провідним ВНЗ доцільно встановити мінімальний рівень балів сертифікатів абітурієнтів з математики та фізики не менше 170 (за існуючою системою рейтингових балів) та надати право проводити додаткові творчі випробування.
- Провідним університетам, метою яких є формування інтелектуальної еліти держави, надати право проводити додаткові творчі випробування, що дозволять їм відібрати «своїх» абітурієнтів, дійсно спроможних і готових до засвоєння глибоких фундаментальних знань.
- У вищих навчальних закладах необхідно створити ефективну систему управління індивідуальною навчальною діяльністю студентів, що має реалізувати прогностичні можливості календарних атестацій студентів та рейтингових систем оцінювання навчальної діяльності студентів.
Список використаної літератури:
- Український центр оцінювання якості освіти. Офіційний звіт про проведення зовнішнього незалежного оцінювання навчальних досягнень випускників загальноосвітніх навчальних закладів України у 2013 році. – Режим доступу: http//www.testportal.gov.ua/reports/