УДК 517.9
Асимптотичні властивості неперервних розв’язків лінійних функціонально-різницевих рівнянь / Блащак Н.І., Сивак О.А. // Наукові вісті НТУУ “КПІ”. – 2013. – № 4. – С. 7–13.
У роботі досліджуються асимптотичні властивості неперервних розв’язків лінійних функціонально-різницевих рівнянь вигляду ![]() у низці випадків залежно від припущень відносно дійсних сталих
у низці випадків залежно від припущень відносно дійсних сталих ![]() і
і ![]() . З використанням методів теорії диференціальних і різницевих рівнянь встановлено нові умови існування неперервних розв’язків лінійних функціонально-різницевих рівнянь, запропоновано метод побудови таких розв’язків, вивчено структуру та поведінку їх множини при
. З використанням методів теорії диференціальних і різницевих рівнянь встановлено нові умови існування неперервних розв’язків лінійних функціонально-різницевих рівнянь, запропоновано метод побудови таких розв’язків, вивчено структуру та поведінку їх множини при ![]() і досліджено властивості залежно від умов, накладених на
і досліджено властивості залежно від умов, накладених на ![]() ,
, ![]() . Зокрема, в теоремі 1 доведено існування сім’ї неперервних обмежених при
. Зокрема, в теоремі 1 доведено існування сім’ї неперервних обмежених при ![]() розв’язків, що залежить від довільної неперервної 1-періодичної функції
розв’язків, що залежить від довільної неперервної 1-періодичної функції ![]() при виконанні умов
при виконанні умов ![]()
![]() і
і ![]()
![]() розв’язки якої зображаються у вигляді ряду (2), де
розв’язки якої зображаються у вигляді ряду (2), де ![]() ,
, ![]() , – деякі неперервні функції, які є розв’язками послідовності рівнянь
, – деякі неперервні функції, які є розв’язками послідовності рівнянь ![]() ,
, ![]() , та задовольняють оцінки (5). Більше цього, за таких же умов щодо дійсних сталих
, та задовольняють оцінки (5). Більше цього, за таких же умов щодо дійсних сталих ![]() і
і ![]() доведено теорему 2 для неоднорідного рівняння та теорему 3 на випадок, коли
доведено теорему 2 для неоднорідного рівняння та теорему 3 на випадок, коли ![]() є деякими дійсними функціями дійсної змінної
є деякими дійсними функціями дійсної змінної ![]() .
.
Ключові слова: функціонально-різницеве рівняння, неперервний розв’язок, асимптотичні властивості, умови існування неперервного розв’язку.
Бібліогр.: 7 назв.
УДК 517.581
Інтегральні рівняння з r -гіпергеометричними функціями / Вірченко Н.О., Ізбаш А.М. // Наукові вісті НТУУ “КПІ”. – 2013. – № 4. – С. 14–18.
Досліджено деякі нові властивості r -гіпергеометричних функцій, зокрема, доведені диференціальні співвідношення для функції ![]() , співвідношення типу Куммера. Отримано інтегральне перетворення Мелліна для r -гіпергеометричної функції
, співвідношення типу Куммера. Отримано інтегральне перетворення Мелліна для r -гіпергеометричної функції ![]() з класичною гіпергеометричною функцією Гаусса
з класичною гіпергеометричною функцією Гаусса ![]() . Доведено формулу зображення r -гіпергеометричної функції
. Доведено формулу зображення r -гіпергеометричної функції ![]() у вигляді дробового інтеграла Рімана–Ліувілля. Подано застосування r -гіпергеометричних функцій до теорії інтегральних рівнянь. Розв’язано інтегральні рівняння Вольтерра першого роду з r -гіпергеометричною функцією в ядрі. Розв’язки цих інтегральних рівнянь отримано в загальній фор-мі за допомогою апарату теорії дробового інтегро-диференціювання.
у вигляді дробового інтеграла Рімана–Ліувілля. Подано застосування r -гіпергеометричних функцій до теорії інтегральних рівнянь. Розв’язано інтегральні рівняння Вольтерра першого роду з r -гіпергеометричною функцією в ядрі. Розв’язки цих інтегральних рівнянь отримано в загальній фор-мі за допомогою апарату теорії дробового інтегро-диференціювання.
Ключові слова: r -гіпергеометрична функція; співвідношення типу Куммера; дробовий інтеграл; інтегральні рівняння Вольтерра першого роду.
Бібліогр.: 5 назв.
УДК 636.631.223.018
r -гіпергеометрична функція і її застосування / Вірченко Н.О., Овчаренко О.В. // Наукові вісті НТУУ “КПІ”. – 2013. – № 4. – С. 19–22.
У роботі за допомогою ![]() -узагальненої виродженої гіпергеометричної функції запроваджено r -гіпергеометричну функцію. Метою цього було вивчення основних властивостей r -гіпергеометричної функції. Зокрема, вивчено співвідношення типу Ердеї, перетворення Мелліна, композиційне співвідношення з оператором типу Ердеї–Кобера. У дослідженні використовувалися загальні методи теорії спеціальних функцій, теорії інтегральних перетворень та операторів дробового інтегрування. Також отримано зображення r -гіпергеометричної функції у вигляді дробового інтеграла. Подано деякі застосування r -гіпергеометричних функцій до розв’язання інтегральних рівнянь Вольтерра в замкнутій формі. Результати роботи можуть бути використані для подальшого розвитку теорії спеціальних функцій та їх застосування в різних науках.
-узагальненої виродженої гіпергеометричної функції запроваджено r -гіпергеометричну функцію. Метою цього було вивчення основних властивостей r -гіпергеометричної функції. Зокрема, вивчено співвідношення типу Ердеї, перетворення Мелліна, композиційне співвідношення з оператором типу Ердеї–Кобера. У дослідженні використовувалися загальні методи теорії спеціальних функцій, теорії інтегральних перетворень та операторів дробового інтегрування. Також отримано зображення r -гіпергеометричної функції у вигляді дробового інтеграла. Подано деякі застосування r -гіпергеометричних функцій до розв’язання інтегральних рівнянь Вольтерра в замкнутій формі. Результати роботи можуть бути використані для подальшого розвитку теорії спеціальних функцій та їх застосування в різних науках.
Ключові слова: r -гіпергеометрична функція; ![]() -узагальнена вироджена гіпергеометрична функція; дробовий інтеграл Рімана–Ліувілля; інтегральні рівняння з гіпергеометричними функціями в ядрах.
-узагальнена вироджена гіпергеометрична функція; дробовий інтеграл Рімана–Ліувілля; інтегральні рівняння з гіпергеометричними функціями в ядрах.
Бібліогр.: 9 назв.
УДК 517.9
Монотонні матричні диференціальні рівняння Ляпунова та Рікатті / Гречко А.Л. // Наукові вісті НТУУ “КПІ”. – 2013. – № 4. – С. 23–26.
Узагальнено теорему Полачека–Терещака для випадку монотонного матричного диференціального рівняння Ляпунова та Рікатті. Встановлено існування одновимірного інваріантного багатовиду для рівняння Ляпунова. Використовуючи метод проективного стиску Гільберта–Біркгоффа в теоремі про нерухому точку, визначено умови, за яких матричне диференціальне рівняння Ляпунова має одновимірний інваріантний багатовид у конусі додатно визначених квадратичних форм. Основним припущенням у цій статті є строга монотонність лінійного розширення динамічної системи на тривіальному векторному розшаруванні. Доведено монотонність матричного диференціального рівняння Ляпунова та Рікатті. Запропонований метод проективного аналогу принципу нерухомої точки в застосуванні до диференціального матричного рівняння Ляпунова зі спеціальною малою правою частиною дає можливість довести існування одновимірного інваріантного багатовиду в конусі додатних квадратичних форм.
Ключові слова: матричне диференціальне рівняння Ляпунова, строго монотонне лінійне розширення.
Бібліогр.: 6 назв.
УДК 517.98
Стохастичні інтеграли по процесу Леві та стохастичні похідні на просторах регулярних основних і узагальнених функцій / Дирів М.М., Качановський М.О. // Наукові вісті НТУУ “КПІ”. – 2013. – № 4. – С. 27–30.
Розширений стохастичний інтеграл Скорохода по процесу Леві та відповідна стохастична похідна Хіди на просторі квадратично інтегровних випадкових величин ![]() мають багато застосувань у стохастичному аналізі, зокрема в теорії стохастичних диференціальних та інтегральних рівнянь. Але іноді (наприклад, для того, щоб розглядати так звані нормально впорядковані стохастичні рівняння) зручно уводити та вивчати ці оператори на деяких просторах основних і узагальнених функцій чи на просторах деякого оснащення
мають багато застосувань у стохастичному аналізі, зокрема в теорії стохастичних диференціальних та інтегральних рівнянь. Але іноді (наприклад, для того, щоб розглядати так звані нормально впорядковані стохастичні рівняння) зручно уводити та вивчати ці оператори на деяких просторах основних і узагальнених функцій чи на просторах деякого оснащення ![]() . Зокрема, у цьому випадку існує можливість визначити зазначені вище оператори як неперервні, вивчати їх зв’язок із так званим віківським численням тощо. В цій статті, використовуючи теорію гільбертових оснащень, ми вводимо та вивчаємо розширені стохастичні інтеграли по процесу Леві та стохастичні похідні Хіди як лінійні неперервні оператори на просторах так званого параметризованого регулярного оснащення
. Зокрема, у цьому випадку існує можливість визначити зазначені вище оператори як неперервні, вивчати їх зв’язок із так званим віківським численням тощо. В цій статті, використовуючи теорію гільбертових оснащень, ми вводимо та вивчаємо розширені стохастичні інтеграли по процесу Леві та стохастичні похідні Хіди як лінійні неперервні оператори на просторах так званого параметризованого регулярного оснащення ![]() . Це дає можливість розширити область застосувань цих операторів.
. Це дає можливість розширити область застосувань цих операторів.
Ключові слова: розширений стохастичний інтеграл; стохастична похідна; процес Леві.
Бібліогр.: 11 назв.
УДК 517.518.3 + 517.518.85
Метод покращення збіжності рядів Фур’є та інтерполяційних багаточленів по ортогональних функціях / Денисюк В.П. // Наукові вісті НТУУ “КПІ”. – 2013. – № 4. – С. 31–37.
Розроблено та досліджено метод покращення збіжності рядів Фур’є по системах ортогональних функцій, застосування якого дає можливість отримувати рівномірно збіжні ряди для гладких функцій, а також метод покращення збіжності інтерполяційних багаточленів по системах ортогональних функцій, який у багатьох випадках дає змогу змен-шити похибки інтерполяції такими багаточленами. Було розроблено методи фантомних функцій і фантомних вузлів, характерною особливістю яких є наближення заданої функції на частині відрізка ортогональності. Розроблені методи досліджувалися на тестовому прикладі для випадку тригонометричних рядів Фур’є і, відповідно, для випадку інтерполяційних тригонометричних багаточленів. Результати наведених досліджень демонструють високу ефективність запропонованих методів. Під час досліджень виявилося, що в деяких випадках метод фантомних вузлів веде до аномального зменшення похибок інтерполяції. Оскільки запропонований метод фантомних вузлів не вкладається повною мірою у сучасну теорію наближень, він вимагає подальших теоретичних досліджень.
Ключові слова: ортогональні системи функцій, ряди Фур’є, покращення збіжності, інтерполяція.
Іл. 4. Табл. 2. Бібліогр.: 5 назв.
УДК 517.983.27
Дослідження закону дистрибутивності в класичній інтервальній арифметиці для загального випадку / Жуковська О.А., Титаренко А.О. // Наукові вісті НТУУ “КПІ”. – 2013. – № 4. – С. 38–44.
Досліджено закон дистрибутивності в класичній інтервальній арифметиці. Дослідження проводилося для інтервальних величин, заданих у формі центр–радіус. Проведено класифікацію інтервалів, на основі якої множина інтервалів подана як об’єднання трьох підмножин, які визначаються співвідношеннями значень центрів і радіусів. Сформульовано умови виконання закону дистрибутивності, які вимагають належності трійки інтервалів і суми двох інтервалів до однієї підмножини. Наведено умови, за яких сума двох інтервалів буде належати до тієї ж підмножини, що й інтервали, які додаються. Доведено теорему, що визначає необхідні та достатні умови виконання закону дистрибутивності для інтервалів, що належать до однієї підмножини. Проведено узагальнення дистрибутивного закону на випадок довільного числа інтервалів. Наведено умови, за яких сума багатьох інтервалів буде належати до тієї ж підмножини, що й інтервали, які додаються. Наведено необхідні та достатні умови виконання узагальненого закону дистрибутивності для інтервалів, які належать до однієї підмножини. Конструктивність отриманих умов продемонстровано на числовому прикладі. Отримані результати дають можливість провести дослідження із вдосконалення алгебричної структури множини інтервалів.
Ключові слова: інтервал, дистрибутивний закон, узагальнення дистрибутивного закону.
Іл. 1. Бібліогр.: 6 назв.
УДК 519.21
Асимптотичні властивості періодограмних оцінок параметрів модульованого майже періодичного сигналу / Жураковський Б.М., Іванов О.В. // Наукові вісті НТУУ “КПІ”. – 2013. – № 4. – С. 45–54.
У статті розглядається задача виявлення прихованих періодичностей. Як моделі корисного сигналу взято модульований майже періодичний сигнал, що спостерігається на фоні випадкового шуму, який є локальним функціоналом від гауcсового стаціонарного процесу із сильною залежністю. Для оцінювання невідомих кутової частоти та амплітуди модульованого сигналу вибрано періодограмні оцінки, для яких було отримано достатні умови консистентності та асимптотичної нормальності і знайдено вигляд їх сумісного граничного нормального розподілу. При отриманні цього результату було використано математичний апарат граничних теорем теорії випадкових процесів, слабкої збіжності деякої сім’ї мір до спектральної міри функції регресії тощо. Новим, порівняно з відомими результатами в теорії періодограмних оцінок у моделях спостереження зі слабко залежним шумом, є розглядання в статті випадкового шуму, який є локальним функціоналом від сильнозалежного гауссового стаціонарного процесу.
Ключові слова:періодограмна оцінка, майже періодичний функція, асимптотична нормальність, сильна залежність, приховані періодичності, нелінійна регресія.
Бібліогр.: 16 назв.
УДК 519.21
Граничні теореми для екстремальних залишків у лінійній моделі регресії з гауссовим стаціонарним шумом / Іванов О.В., Приходько В.В. // Наукові вісті НТУУ “КПІ”. – 2013. – № 4. – С. 55–62.
Розглянуто лінійну модель регресії з неперервним часом і гауссовим стаціонарним сильнозалежним випадковим шумом. Досліджено поведінку нормованих певним чином екстремальних залишків, тобто максимальних різниць або їх абсолютних величин, між спостереженнями та значеннями функції регресії, в яку замість невідомої величини параметра підставлено його оцінку найменших квадратів. Для лінійної моделі регресії отримано умови слабкої збіжності нормованих екстремальних залишків до подвійної експоненти, що є наслідком припущення про гауссовість випадкового шуму. При цьому в нормуючі функції замість невідомих дисперсії та 2-го спектрального момента гауссового стаціонарного шуму підставлено консистентні оцінки вказаних параметрів. Оцінка дисперсії шуму є узагальненням залишкової суми квадратів класичної математичної статистики, а оцінка 2-го спектрального моменту узагальнює оцінку Ліндгрена. У роботі використано математичний апарат статистики випадкових процесів і граничних теорем для екстремумів гауссових стаціонарних процесів. Отримані нові результати дають можливість будувати нетрадиційні статистичні критерії перевірки адекватності регресійної моделі.
Ключові слова:лінійна модель регресії, екстремальні залишки, слабка збіжність, гауссов стаціонарний шум, оцінки дисперсії та другого спектрального моменту, консистентність оцінок.
Бібліогр.: 12 назв.
УДК 519.21
PRV-умови необмеженості розв’язку стохастичного диференціального рівняння / Клесов О.І., Тимошенко О.А. // Наукові вісті НТУУ “КПІ”. – 2013. – № 4. – С. 63–66.
Досліджено асимптотичну поведінку розв’язку стохастичного диференціального рівняння ![]()
![]()
![]() де
де ![]() – стандартний вінерів процес;
– стандартний вінерів процес; ![]() – невипадкова додатна стала;
– невипадкова додатна стала; ![]() – розв’язок рівняння,
– розв’язок рівняння, ![]() та
та ![]() – неперервні функції. Знайдено умови на функції
– неперервні функції. Знайдено умови на функції ![]() та
та ![]() при яких розв’язок
при яких розв’язок ![]() прямує до нескінченності. Необмеженість розв’язку є важливим питанням при вивченні асимптотичної поведінки розв’язку стохастичного диференціального рівняння. Основні результати, що стосуються необмеженості розв’язку для автономногостохастичного диференціального рівняння, були отримані Й.І. Гіхманом та А.В. Скороходом. У статті доведено деякі достатні умови, за яких розв’язок неавтономного стохастичного диференціального рівняння прямує до нескінченності при
прямує до нескінченності. Необмеженість розв’язку є важливим питанням при вивченні асимптотичної поведінки розв’язку стохастичного диференціального рівняння. Основні результати, що стосуються необмеженості розв’язку для автономногостохастичного диференціального рівняння, були отримані Й.І. Гіхманом та А.В. Скороходом. У статті доведено деякі достатні умови, за яких розв’язок неавтономного стохастичного диференціального рівняння прямує до нескінченності при ![]() Знайдено деякі достатні умови необмеженості розв’язку неавтономного стохастичного диференціального рівняння в термінах PRV-функцій. Дослідження проведено на основі PRV-теорії, яку було розроблено в серії праць В.В. Булдигіна, О.І. Клесова, Й.Г. Штайнебаха.
Знайдено деякі достатні умови необмеженості розв’язку неавтономного стохастичного диференціального рівняння в термінах PRV-функцій. Дослідження проведено на основі PRV-теорії, яку було розроблено в серії праць В.В. Булдигіна, О.І. Клесова, Й.Г. Штайнебаха.
Ключові слова: стохастичне диференціальне рівняння, необмеженість розв’язку, функції регулярної зміни.
Бібліогр.: 11 назв.
УДК 517.95
Попередня групова класифікація одного класу узагальнених лінійних рівняннь Колмогорова / Коваленко С.С., Копась І.М., Стогній В.І. // Наукові вісті НТУУ “КПІ”. – 2013. – № 4. – С. 67–72.
Одним із сучасних методів дослідження як лінійних, так і нелінійних диференціальних рівнянь із частинними похідними є теоретико-груповий метод, який дає можливість конструктивно будувати точні часткові класичні розв’язки тих рівнянь, які допускають нетривіальну групу симетрій. У цій статті розглядається один клас (2+1)-вимірних узагальнених лінійних рівнянь Колмогорова. Мета роботи – дослідити симетрійні властивості рівнянь з цього класу та застосувати їх для побудови інваріантних фундаменталь-них розв’язків. За алгоритмом Ахатова–Газізова–Ібрагімова проведено попередню групову класифікацію досліджуваного класу диференціальних рівнянь. Для отриманих рівнянь з нетривіальними симетрійними властивостями знайдено максимальні алгебри інваріантності. За алгоритмом Аксьонова обчислено алгебру інваріантності фундаментальних розв’язків лінійного рівняння Колмогорова, оператори якої були використані для побудови інваріантних фундаментальних розв’язків цього рівняння. Показано, що фундаментальний розв’язок, отриманий А.М. Колмогоровим, є інваріантним фундаментальним розв’язком лінійного рівняння Колмогорова.
Ключові слова: групова класифікація, лінійне рівняння Колмогорова, алгебра інваріантності, перетворення еквівалентності, інваріантний розв’язок, фундаментальний розв’язок.
Табл. 1. Бібліогр.: 13 назв.
УДК 517.9
Обернена спектральна задача для блочних матриць типу Якобі, відповідних дійсній двовимірній проблемі моментів / Козак В.І. // Наукові вісті НТУУ “КПІ”. – 2013. – № 4. – С. 73–76.
Метою роботи є знаходження матриць, які б відповідали деякій скінченній мірі з компактним носієм на дійсній площині, тобто потрібно розв’язати обернену спектральну задачу для дійсної двовимірної проблеми моментів (на дійсній площині). Було визначено матрицю Якобі, відповідну дійсній двовимірній проблемі моментів, а також систему ортонормованих поліномів відносно деякої міри з компактним носієм на дійсній площині, яку було отримано в результаті ортогоналізації за Шмідтом в певному порядку двохіндексної множини функцій (індекси належать множині натуральних чисел, включаючи нуль) з визначеними властивостями. Також отримано пару матриць з блочною тридіагональною структурою, які діють у просторі типу ![]() як алгебрично комутуючі самоспряжені обмежені оператори, та визначено деякі їх властивості. Випадки попередніх досліджень є частинними відносно описаного в статті.
як алгебрично комутуючі самоспряжені обмежені оператори, та визначено деякі їх властивості. Випадки попередніх досліджень є частинними відносно описаного в статті.
Ключові слова: обернена спектральна задача, блочні матриці типу Якобі, дійсна двовимірна проблема моментів.
Бібліогр.: 7 назв.
УДК 519.95
Застосування апарату теорії дробового числення до інтегральних операторів із узагальненими гіпергеометричними функціями / Овчаренко О.В. // Наукові вісті НТУУ “КПІ”. – 2013. – № 4. – С. 77–82.
У статті досліджувалися властивості інтегральних операторів з узагальненими гіпергеометричними функціям в ядрі, зокрема вивчалися умови існування та їх обмеженості, досліджувалися композиційні співвідношення з дробовими інтегралами. При досліджені використано загальні методи теорії спеціальних функцій, теорії інтегральних перетворень і операторів дробового інтегро-диференціювання. Запроваджено інтегральні оператори з (t,b)-узагальненими гіпергеометричними функціями в ядрі. Для цих операторів одержано функціональні співвідношення, досліджено умови існування та обмеженості в просторі Лебега. Також отримано композиційні співвідношення для запроваджених інтегральних операторів з лівостороннім дробовим інтегралом Рімана–Ліувілля. Застосовано апарат теорії дробового числення до узагальнених гіпергеометричних функцій, а саме: одержано функціональні співвідношення, що демонструють дію лівосторонніх дробових інтеграла та похідної Рімана–Ліувілля на (t,b)-узагальнену за Райтом гіпергеометричну функцію Гаусса і (t,b)-узагальнену конфлюентну гіпергеометричну функцію. Отримані результати можна використати для подальшого розвитку теорії спеціальних функцій та їх широкого застосування.
Ключові слова: (t,b)-узагальнена гіпергеометрична функція; конфлюентна гіпергеометрична функція; дробові похідна та інтеграл Рімана–Ліувілля; інтегральні оператори з гіпергеометричними функціями в ядрі.
Бібліогр.: 12 назв.
УДК 517.98+517.854
Варіаційний підхід до задачі Діріхле з лапласіаном по мірі на гільбертовому просторі / Санжаревський Я.Ю. // Наукові вісті НТУУ “КПІ”. – 2013. – № 4. – С. 83–87.
Досліджено задачу Діріхле для еліптичного рівняння в області гільбертового простору. Зокрема, сформульовано задачу Діріхле для рівняння, що розглядається, а також слабкої версії задачі, яка передбачає пошук слабких розв’язків. Сформульовано та доведено теореми існування та єдиності слабкої версії першої крайової задачі та, окремо, вихідної версії поставленої задачі у спільній області визначення лівої та правої частин вихідного рівняння. Причому слабку версію задачі розв’язано за допомогою варіаційного підходу. Для розв’язку задачі використовувалися методи функціонального аналізу та, зокрема, теорема Рісса, а також широко використовувана теорія необмежених лінійних операторів. Успішність дослідження та розв’язання першої крайової задачі для розглянутого рівняння з введеною раніше Ю.В. Богданським версією нескінченновимірного оператора Лапласа по мірі дає можливість розраховувати на успішність дослідження другої та третьої крайових задач для рівняння, що розглядається, в області гільбертового простору.
Ключові слова: гільбертів простір, борелівська міра, диференціювання мір, еліптичні рівняння, оператор Лапласа, оператор сліда, задача Діріхле.
Бібліогр.: 6 назв.
УДК 517.95
Групова класифікація нелінійних рівнянь колмогорівського типу / Сєров М.І., Спічак С.В., Стогній В.І., Рассоха І.В. // Наукові вісті НТУУ “КПІ”. – 2013. – № 4. – С. 88–93.
Розглядаються нелінійні рівняння колмогорівського типу, в які входить довільна функція. Одним із методів розв’язування диференціальних рівнянь з частинними похідними є теоретико-груповий метод. За допомогою цього методу вдається проінтегрувати ті рівняння, які мають нетривіальну групу симетрії. Тому задача групової класифікації є актуальною. Проведено групову класифікацію нелінійних рівнянь колмогорівського типу. За допомогою знайдених неперервних перетворень еквівалентності виділені нееквівалентні підкласи цих рівнянь. Для всіх підкласів обчислені максимальні алгебри інваріантності. З використанням знайдених підалгебр алгебри інваріантності для деяких нелінійних рівнянь зроблено симетрійну редукцію до рівнянь з меншою кількістю незалежних змінних. Вдалося проінтегрувати редуковані рівняння та отримати точні розв’язки відповідних нелінійних рівнянь.
Ключові слова: групова класифікація, нелінійне рівняння колмогорівського типу, алгебра інваріантності, перетворення еквівалентності, симетрійна редукція, інваріантний розв’язок.
Табл. 1. Бібліогр.: 16 назв.
УДК 512.543
Твірні та співвідношення силовських p-підгруп групи 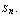 / Скуратовський Р.В. // Наукові вісті НТУУ “КПІ”. – 2013. – № 4. – С. 94–105.
/ Скуратовський Р.В. // Наукові вісті НТУУ “КПІ”. – 2013. – № 4. – С. 94–105.
Досліджено подання силовських р-підгруп групи підстановок у вигляді твірних і співвідношень. Це дало можливість вивчити всі силовські підгрупи інших груп, бо кожна скінченна силовська р-підгрупа ізоморфно занурена в силовську р-підгрупу деякої симетричної групи. Знайдено співвідношення для фіксованої системи твірних, запропонованої в статтi, а також доведено, що ця система співвідношень є мінімальною для вибраної системи твірних. Під час дослідження застосовувався метод канонічних слів і переписування Шраєра. Доведено, що ці підгрупи є скінченнозаданими, тобто мають скінченну кількість твірних і співвідношень. Виявлено тісний зв’язок таких підгруп з ітерованим вінцевим добутком циклічних груп простого порядку, тому він став предметом дослідження. Також йдеться про ітерований вінцевий добуток, який пов’язаний з групою скінченних автоматних перетворень. Описано структурні властивості силовських р-підгруп симетричних груп степеня ![]() тобто
тобто ![]() які частково вже досліджено. Зокрема, вивчено комутанти і породжені ними вербальні підгрупи. Побудовано сферичну функцію росту для силовських підгруп групи
які частково вже досліджено. Зокрема, вивчено комутанти і породжені ними вербальні підгрупи. Побудовано сферичну функцію росту для силовських підгруп групи ![]() Знайдено козображення для силовських p-підгруп груп
Знайдено козображення для силовських p-підгруп груп ![]() а головним результатом є знайдене козображення для силовських p-підгруп груп
а головним результатом є знайдене козображення для силовських p-підгруп груп ![]()
Ключові слова: cиловська підгрупа, вінцевий добуток, співвідношення і твірні.
Бібліогр.: 8 назв.
УДК 537.63; 537.84; 544.63
Рух електроліту при травленні й осадженні металів у неоднорідному постійному магнітному полі / Горобець О.Ю., Горобець Ю.І., Роспотнюк В.П. // Наукові вісті НТУУ “КПІ”. – 2013. – № 4. – С. 106–113.
Розглянуто особливості руху електроліту в приповерхневому шарі в процесах травлення й осадження металів на феромагнітний електрод у формі кулі, намагнічений у зовнішньому однорідному магнітному полі помірної напруже-ності (~ 1 кЕ). Вибір електрода у формі кулі дає можливість у такій модельній системі легко відокремити ефекти магнітного поля від ефектів іншої природи завдяки еквівалентності всіх точок його поверхні за відсутності намагнічування. Показано, що під дією неоднорідних магнітостатичних полів розсіювання намагніченої феромагнітної кулі виникає неоднорідний розподіл концентрації парамагнітних або ефективно парамагнітних кластерних продуктів електрохімічних реакцій в електроліті, наприклад у формі мікро- або нанобульбашок, стабілізованих парамагнітними або діамагнітними іонами, та колоїдних частинок з їх іонним оточенням. Знайдено концентраційну ЕРС, густину струму в електроліті та функціональний вираз для швидкості обертання електроліту під дією сили Лоренца у приповерхневому шарі намагніченої сталевої кулі у площині, перпендикулярній до напрямку зовнішнього магнітного поля, а також рівняння, яке описує поверхню розділення областей електроліту із протилежними напрямками обертання. Результати теоретичного моделювання роботи можуть бути застосовані для створення функціональних матеріалів методами магнітоелектролізу та для моделювання впливу біогенних магнітних наночастинок на транспортні процеси й біохімічні реакції в клітинах живих організмів.
Ключові слова: магнітогідродинамічне перемішування, магнітоелектроліз, ефективна парамагнітна сприйнятливість, градієнтна магнітна сила, сила Лоренца, мікро- та нанобульбашки.
Іл. 1. Бібліогр.: 25 назв.
УДК 539.2:678.01:539.2:537.212
Вплив магнітного поля на структуру і властивості полімерів та їх композитів / Демченко В.Л., Штомпель В.І., Рябов С.В., Унрод В.І. // Наукові вісті НТУУ “КПІ”. – 2013. – № 4. – С. 114–120.
Огляд присвячено впливу магнітного поля на структуру і властивості полімерів та їх композитів. Аналіз проведених досліджень впливу магнітних полів на ненаповнені полімери та композити на їх основі дає можливість розмежувати ефекти, пов’язані із взаємодією полімерної матриці з магнітним полем, і ефекти, зумовлені структуруванням феромагнітних наповнювачів. Встановлено, що під впливом магнітного поля змінюється структура полімерних композиційних матеріалів, що виражається в анізотропному розподілі феромагнітних наповнювачів і призводить до зміни магнітних властивостей полімерів. Показано, що магнітне поле є ефективним засобом регулювання структури і властивостей полімерів та їх композитів як при синтезі, так і при фізико-хімічних способах їх модифікації. Механізм впливу магнітного поля та його ефективність залежать від магнітних властивостей матеріалу.
Ключові слова: магнітне поле, напруженість магнітного поля, полімерний композит, структура, фізико-механічні властивості.
Бібліогр.: 34 назви.
УДК 537.612
Особливості формування нематичної фази в магнетику з S = 2 / Космачов О.О. // Наукові вісті НТУУ “КПІ”. – 2013. – № 4. – С. 121–126.
Досліджено нематичну фазу ізотропного негейзенбергівського магнетика зі спіном магнітного іона 2. Вивчено поведінку спектрів елементарних збуджень в околі ліній фазових переходів з іншими фазами, що реалізуються у цій моделі. Для розв’язку одновузлової задачі використано метод діагоналізації гамільтоніана N-рівневої системи, в основі якого лежить використання алгебри операторів Хаббарда. В результаті досліджень встановлено, що в розглянутій нематичній фазі геометричним образом фази є “гофрований” двохосьовий еліпсоїд через додатковий параметр ![]() Аналіз спектрів на лініях фазового переходу та додаткового аналізу вільної енергії з урахуванням теплових флуктуацій дають можливість уточнити параметр
Аналіз спектрів на лініях фазового переходу та додаткового аналізу вільної енергії з урахуванням теплових флуктуацій дають можливість уточнити параметр ![]() Також показано, що нематична фаза розпадається на “осьову” і “площинну” фази. Проведені дослідження дали змогу уточнити фазову діаграму ізотропного негейзенбергівського магнетика з S = 2.
Також показано, що нематична фаза розпадається на “осьову” і “площинну” фази. Проведені дослідження дали змогу уточнити фазову діаграму ізотропного негейзенбергівського магнетика з S = 2.
Ключові слова: негейзенбергівський магнетик, фазові переходи, оператори Хабарда, нематична фаза, тетраедрична фаза.
Іл. 3. Бібліогр.: 12 назв.
УДК 301.17.15; 532.5;551:465
Генерація компактного турбулентного вихору: наближена модель для відносно великих моментів часу / Лук’янов П.В. // Наукові вісті НТУУ “КПІ”. – 2013. – № 4. – С. 127–131.
Метою досліджень є розроблення аналітичної моделі, що здатна наближено описувати генерацію компактного турбулентного вихору джерелом циркуляції скінченної потужності для відносно великих моментів часу. Методика реалізації базується на градієнтній моделі турбулентності Буссінеска, згідно з якою коефіцієнт турбулентної дифузії отримується як стала величина. Результати досліджень показали невелику відмінність аналітичного розв’язку модельної задачі зі сталим коефіцієнтом турбулентної дифузії від спостережуваної в експерименті розвинутої турбулентної течії (Тейлора–Куетта), якій відповідає, крім відносно дуже тонких граничних шарів, зазначене стале значення. Запропоновано просту модель генерації турбулентного вихору. Її можна застосовувати для відносно великих моментів безрозмірного часу, коли кількісно течія по суті вже є квазістаціонарною. Отриманий розв’язок неможна використовувати для задач турбулентної дифузії за умови припинення дії джерела циркуляції – при цьому не виконується основне припущення щодо сталості коефіцієнта турбулентної в’язкості.
Ключові слова: компактний вихор, генерація, наближена модель.
Іл. 2. Бібліогр.: 14 назв.
УДК 533.63, 534.23
Шум взаємодії вихору і лопаті гелікоптера / Лук’янов Петро В. // Наукові вісті НТУУ “КПІ”. – 2013. – № 4. – С. 132–136.
Розглянуто модель генерації шуму взаємодії вихор–лопать (BVI) ротора гелікоптера в дозвуковому діапазоні швидкостей (![]() ). Визначено кількісні межі застосування цієї моделі. На підставі повного тривимірного рівняння нестаціонарного поширення малих збурень розв’язано задачу про генерацію шуму від взаємодії лопаті ротора гелікоптера параболічної форми та вихору Тейлора, який розміщений на певній відстані над лопаттю. Для розв’язання цієї задачі використовувався числово-аналітичний метод, який дає можливість отримати значення звукового потенціалу та його похідних у ближньому полі. Аналіз розрахунку коефіцієнта тиску показав, що характер взаємодії вихор–лопать породжує три сплески тиску типу ударних хвиль А, В, С, що вперше експериментально встановлені Г. Тьєманом. Але амплітуди цих сплесків менші за рівнем тих, що спостерігались для трансзвукового діапазону швидкостей. Також встановлено, що рівень BVI-шуму вищий, ніж рівень шуму обертання за відсутності вихору, на 10 Дб (відносно рівня
). Визначено кількісні межі застосування цієї моделі. На підставі повного тривимірного рівняння нестаціонарного поширення малих збурень розв’язано задачу про генерацію шуму від взаємодії лопаті ротора гелікоптера параболічної форми та вихору Тейлора, який розміщений на певній відстані над лопаттю. Для розв’язання цієї задачі використовувався числово-аналітичний метод, який дає можливість отримати значення звукового потенціалу та його похідних у ближньому полі. Аналіз розрахунку коефіцієнта тиску показав, що характер взаємодії вихор–лопать породжує три сплески тиску типу ударних хвиль А, В, С, що вперше експериментально встановлені Г. Тьєманом. Але амплітуди цих сплесків менші за рівнем тих, що спостерігались для трансзвукового діапазону швидкостей. Також встановлено, що рівень BVI-шуму вищий, ніж рівень шуму обертання за відсутності вихору, на 10 Дб (відносно рівня ![]() ). Чисельно встановлено, що гранично допустима відстань, на якій ця модель працює, становить
). Чисельно встановлено, що гранично допустима відстань, на якій ця модель працює, становить ![]() (
(![]() – радіус ядра вихору). Зі зростанням відстані між вихором і лопаттю кількісна відмінність помітно зменшується.
– радіус ядра вихору). Зі зростанням відстані між вихором і лопаттю кількісна відмінність помітно зменшується.
Ключові слова: взаємодія вихор–лопать, генерація звуку.
Іл. 4. Бібліогр.: 12 назв.
УДК 538.911
Квантово-механічні структури з дельта-функціональним потенціалом / Нелін Є.А., Водолазька М.В. // Наукові вісті НТУУ “КПІ”. – 2013. – № 4. – С. 137–144.
На основі концепції квантово-механічного імпедансу для розв’язання прикладних задач наноелектроніки розроблено модель імпедансних квантово-механічних d-неоднорідностей – d-бар’єра і d-ями. Розглянуто типові моделі для природних і штучних квантово-механічних структур: поодинокі, подвійні і потрійні d-неоднорідності; потенціальні сходинки, ями і бар’єри з d-неоднорідностями; ґрати d-неоднорідностей. Отримано аналітичні вирази для власних значень структур. Наведено енергетичні залежності коефіцієнтів відбиття та проходження для характерних квантово-механічних структур з d-функціональним потенціалом. Похибку d-моделі проаналізовано порівнянням з характеристиками неоднорідностей зі скінченними розмірами. Розглянуто кристал і кристалоподібну структуру, дефекти в кристалі та поверхневі рівні. Наведено характеристики ґраток d-бар’єрів, які ілюструють зонний характер пропускання необмеженої періодичної структури. Імпедансні d-моделі квантово-механічних структур відрізняються простотою і наочністю, широкими можливостями їх використання при проектуванні наноелектронних пристроїв обробки сигналів, а також у навчальному процесі.
Ключові слова: квантово-механічні структури, дельта-функціональний потенціал, квантово-механічний імпеданс, модель імпедансних d-неоднорідностей, d-функція, d-бар’єр, d-яма.
Іл. 7. Бібліогр.: 6 назв.
УДК 531.32
Інверсія розв’язку Дідіона в задачі балістики матеріальної точки / Ольшанський В.П., Ольшанський С.В. // Наукові вісті НТУУ “КПІ”. – 2013. – № 4. – С. 145–147.
Розроблено зручний спосіб розрахунку дальності (горизонтальної проекції траєкторії) польоту матеріальної точки в газовому середовищі з квадратичним опором рухові по пологій траєкторії. Відомий в теорії балістики розв’язок Дідіона перетворено до вигляду, зручного для розрахунку дальності польоту матеріальної точки в газовому середовищі. Обчислення дальності польоту точки по пологій траєкторії запропоновано проводити за таблицею функції Ламберта. Використання побудованої інверсії розв’язку Дідіона та таблиці функції Ламберта значно спрощує обчислення дальності польоту матеріальної точки по пологій траєкторії. Інверсія розв’язку Дідіона є двозначною, що узгоджується з наявністю на траєкторії висхідної та спадної ділянок. Інверсія може бути використана не тільки для обчислення дальності польоту матеріальної точки, а й для ідентифікації коефіцієнта квадратичного опору середовища, за результатами вимірювань параметрів траєкторії.
Ключові слова: інверсія розв’язку Дідіона, квадратичний опір, функція Ламберта.
Іл. 1. Табл. 2. Бібліогр.: 10 назв.
УДК 621.793:539.23
“Пряма задача” й “обернена задача” в інженерному конструюванні матеріалів / Сидоренко С.І., Замулко С.О. // Наукові вісті НТУУ “КПІ”. – 2013. – № 4. – С. 148–151.
У статті проаналізовано задачі, пов’язані з “конструюванням” нових матеріалів, що останнім часом мають застосування в матеріалознавстві у зв’язку із формуванням ідеології “конструювання нових знань на основі вже накопичених знань”, а також у зв’язку із широким залученням інженерних технологій і оперуванням матеріалознавчими базами даних. Показано, що загальну задачу з інженерного “конструювання” матеріалів необхідно розділити на 3 задачі. Метою розв’язання “прямої задачі” є побудова інтерполяційного полінома на основі наявних дискретних баз даних матеріалознавства. Їх накопичення, аналіз і алгоритми оперування ними – відносно самостійна задача. Коли “пряму задачу” вже розв’язано (інтерполяційний поліном побудовано), тоді з використанням цього полінома може розв’язуватися і “обернена задача”: які склади матеріалу можуть забезпечити отримання наперед заданих властивостей (“обернена задача 1-го роду”). Розв’язання “оберненої задачі” може бути здійснене й через квантово-імітаційне моделювання, наприклад “із перших принципів”. При цьому на рівняння Шредінгера накладаються певні обмеження, а в результаті його розв’язання дослідник отримує склади, що забезпечують наперед задані властивості за умов накладених обмежень (“обернена задача 2-го роду”). Розв’язання цих задач для конкретних систем дасть змогу прискорити створення нових матеріалів із наперед заданими властивостями.
Ключові слова: інженерне конструювання матеріалів, матеріалознавчі бази даних, пряма задача, обернена задача, нові матеріали з наперед заданими властивостями.
Іл. 1. Бібліогр.: 22 назви.
УДК 53.05,06,08; 51-7, 519.1
Критичні явища в графі динамічної видимості / Снарський А.О., Безсуднов І.В. // Наукові вісті НТУУ “КПІ”. – 2013. – № 4. – С. 152–156.
Вивчено часові ряди зі складною, в т.ч. фрактальною, структурою. Показано, що метод аналізу, запропонований авторами – граф динамічної видимості, веде до характеристики, яка поводиться аналогічно до параметра порядку в теорії фазових переходів другого роду. У рамках цього методу розглянуто поведінку відносної кількості кластерів поблизу критичного значення кута зору. Чисельно досліджено часові ряди різної природи: як модельні (однорідний випадковий розподіл, розподіл Пуассона і модифікація ряду Вейєрштрасса), так і експериментальні (RR-інтервали серцевого ритму людини, ряд даних по сонячних спалахах і часовий ряд землетрусів). У всіх випадках залежність кількості кластерів від близькості до критичного кутку зору була ступеневою. Таким чином, було показано існування аналогії між поведінкою відносної кількості кластерів та параметра порядку в теорії фазових переходів другого роду. Кожен ряд характеризується своїм числовим значенням критичного індексу – аналога критичного індексу в теорії фазових переходів.
Ключові слова: часові ряди, графи видимості, критичні явища.
Іл. 3. Бібліогр.: 16 назв.
| Долучення | Розмір |
|---|---|
| Научные вести НТУУ "КПИ". № 4. 2013 (реферат) [nv-abstract-13-4_ru.pdf (449.16 КБ)] (449.16 КБ) | 449.16 КБ |
| Naukovi visti NTUU “КPІ”. – 2013. – N 4 (abstract) [nv-abstract-13-4_en.pdf (231.13 КБ)] (231.13 КБ) | 231.13 КБ |
