Цієї осені наша газета вже двічі (15 жовтня і 12 листопада) розповідала про наукові здобутки Почесного доктора КПІ ім. Ігоря Сікорського, лауреата Нобелівської премії 2020 року з фізики Роджера Пенроуза. Спочатку про ті, за які присуджено премію, згодом про "неможливі об'єкти Пенроуза", які дали певний поштовх у виникненні нового напряму в мистецтві – імпоссибілізму. Сьогодні розповідаємо про "мозаїки Пенроуза", які теж могли б вважатися неможливими, якби їх не існувало.
Відомо, що площину можна розбити на тотожні квадрати, трикутники, шестикутники, ромби, які утворять узор, що характеризується не лише поворотною, але й трансляційною (елементи мозаїки періодично повторюються) симетрією. Таку саму властивість може мати розбиття площини на фігури кількох типів, скажімо, восьмикутники і квадрати. У середині ХХ сторіччя математики почали шукати відповідь на питання: чи можна створити неперіодичну мозаїку, і якою може бути мінімальна кількість видів геометричних фігур, які її утворюють?
На початку 70-х рр. цю проблему вирішив Роджер Пенроуз – професор математики Оксфордського університету, створивши неперіодичні мозаїки, які було названо його ім'ям – "неперіодичні мозаїки Пенроуза".
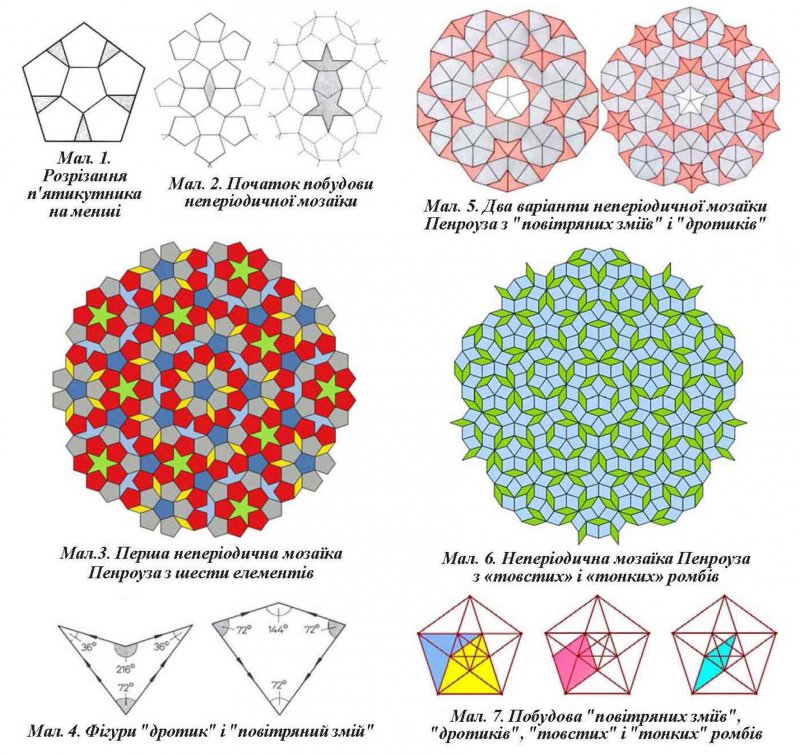
У 1978 р. у своїй статті "Pentaplexity. A Class of Non-Periodic Tilings of the Plane" ("Пентаплексичність. Клас неперіодичних розбиттів площини") він описав, як шукав і знайшов ці мозаїки. Спершу Пенроуз звернув увагу на те, що правильний п'ятикутник можна розрізати на шість менших п'ятикутників і п'ять трикутників (мал. 1). При цьому він зауважив, що з'єднані таким чином шість п'ятикутників є частиною відомої розгортки додекаедра. Далі він почав розмірковувати, як можна замостити площину цими п'ятикутниками. Розпочав з варіантів, показаних на мал. 2 і шукав фігури, якими можна заповнити проміжки між п'ятикутниками. В результаті створив свою першу неперіодичну мозаїку (мал. 3), яка складається з шести елементів: п'ятикутної зірки, ромба, "паперового кораблика" і трьох видів п'ятикутників (позначені різним кольором). Далі він став досліджувати отриману мозаїку і шукати, яким чином можна було б об'єднати якісь дві сусідні фігури в одну, щоб зменшити кількість різних елементів. Цим способом він спочатку отримав неперіодичну мозаїку з п'яти елементів, потім з чотирьох, а далі, розрізавши отримані фігури на частини і об'єднавши частини в нові фігури, Пенроуз побудував мозаїку з двох чотирикутників, які, за пропозицією Дж.Конвея, називаються "повітряним змієм" (Kite) і "дротиком" (Dart) (мал. 4 і 5). Цікаво зазначити, що відношення довжини більших сторін цих чотирикутників до довжини менших сторін дорівнює золотому перетину (1,6180339…). Далі Пенроуз визначив, що з цих елементів можна утворити кілька різних неперіодичних мозаїк (дві з них наведено на малюнку). Аналізуючи ці мозаїки, Пенроуз довів, що на нескінченній площині відношення кількості "повітряних зміїв" до кількості "дротиків" дорівнює золотому перетину. А оскільки це число є ірраціональним, то це означає, що мозаїка з таких елементів є неперіодичною. До речі, згадана стаття Пенроуза є у вільному доступі в Інтернеті.
Далі Роджер Пенроуз дійшов думки, що неперіодичну мозаїку можна утворити з двох ромбів: "товстого", який має кути 72 і 108 градусів, і "тонкого" з кутами 36 і 144 градуси (мал. 6). Ці, як і попередні "неперіодичні мозаїки Пенроуза", мають цікаву особливість: вони симетричні відносно осі п'ятого порядку. До їх створення були відомі мозаїки лише з осями симетрії третього, четвертого, шостого порядків, оскільки правильними п'ятикутниками замостити площину неможливо.
Цікаво зазначити, що чотири елементи, з яких утворюються "неперіодичні мозаїки Пенроуза", можна легко отримати, намалювавши правильний п'ятикутник і виконавши в ньому прості геометричні побудови (мал. 7).
Створивши неперіодичні мозаїки, Пенроуз не став надсилати статтю про них у наукові журнали. Він розумів, що його мозаїки можуть мати різноманітне застосування і становлять комерційну цінність. Тому вирішив спочатку запатентувати їх у Великобританії, США і Японії, а вже після того публікувати статті. Таким чином, він має, зокрема, патент США №4133152 "Set of tiles for covering a surface" ("Набір плиток для покриття поверхні"). Там описано плитки, що мають форму "повітряних зміїв", "дротиків", "товстого" і "тонкого" ромбів, а також плитки, отримані з них шляхом перетворення прямих сторін вихідних плиток на криві. Найцікавіший приклад таких плиток із наведених у патенті відомий нині як "курчата Пенроуза". В патенті також подається опис ігор, де використовуються подібні плитки.
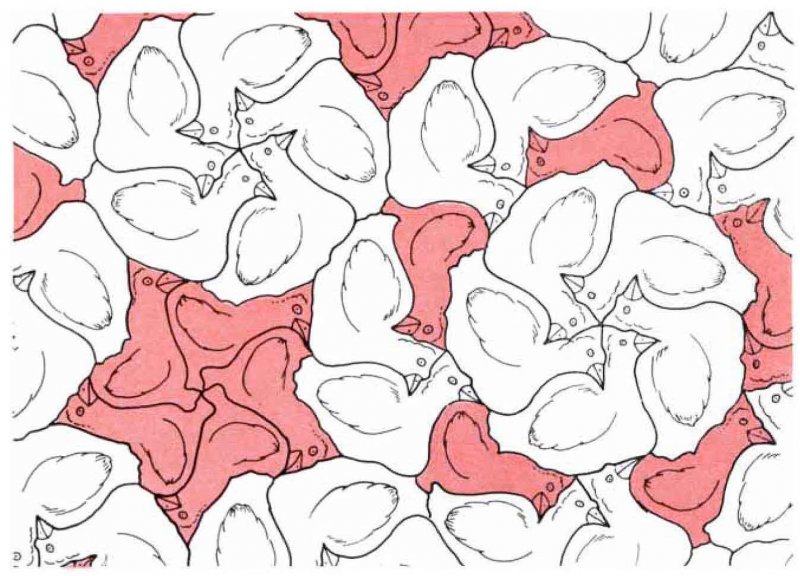
Неперіодичні мозаїки Пенроуза нині стали досить поширеними. "Плитками Пенроуза" замощують підлоги, тротуари, прикрашають стіни, випускають їх набори як головоломки. Це невипадково. Математики знають, що приховану красу математичних результатів відчувають і люди, які не вивчали математику. А у мозаїках Пенроуза поєднані і прихована, і видима краса.


